next up previous index
Next:  Метод моментов  Up:  Точечное оценивание  Previous:  Параметрические семейства распределений

2.2.   Точечные оценки. Несмещенность, состоятельность оценок

Итак, пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из параметрического семейства распределений $\mathscr F_\theta$, $\theta \in \Theta$.

   Заметим, что все характеристики случайных величин $X_1$, $\ldots$, $X_n$зависят от параметра $\theta$. Так, например, для $X_i$ с распределением Пуассона $\text{\boldmath\ensuremath \Pi}_\lambda$

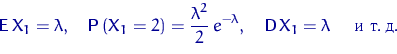
\begin{displaymath} {\mathsf E}\, X_1 = \lambda, \quad {\mathsf P}\,(X_1 = 2) = ... ...da}, \quad {\mathsf D}\, X_1 = \lambda \quad \textrm{ и т.\,д.}\end{displaymath}

  Чтобы отразить эту зависимость, будем писать ${\mathsf E}_\theta\, X_1$ вместо ${\mathsf E}\, X_1$ и т.д. Так, ${\mathsf D}\,{\!}_{\theta_1} X_1$ означает дисперсию, вычисленную в предположении $\theta=\theta_1$.

  Во многих случаях эта условность необходима. Предположим, что $X_i$ имеют распределение Пуассона $\text{\boldmath\ensuremath \Pi}_\lambda$. В предположении, что $\lambda=1$, имеем ${\mathsf E}\, X_1=1$, тогда как при $\lambda=7$ имеем ${\mathsf E}\, X_1=7$. Таким образом, запись ${\mathsf E}\, X_1$, без указания на распределение $X_1$, оказывается просто бессмысленной.

Определение 2.

Статистикой называется произвольная функция $\theta^*=\theta^*(X_1, \ldots, X_n)$ от элементов выборки.

Замечание 5.

Статистика есть функция от эмпирических данных, но никак не от параметра $\theta$. Статистика, как правило, предназначена именно для оценивания неизвестного параметра $\theta$ (поэтому ее иначе называют «оценкой»), и уже поэтому от него зависеть не может.

Конечно, статистика есть не «любая», а «измеримая» функция от выборки (борелевская, для которой прообраз любого борелевского множества из ${\textrm{\upshape I\kern-0.20em R}}$ есть снова борелевское множество в ${\textrm{\upshape I\kern-0.20em R}}^n$), но мы никогда не встретимся с иными функциями, и более на это обращать внимание не будем.

Определение 3.

Статистика $\theta^*=\theta^*(X_1, \ldots, X_n)$ называется несмещенной оценкой параметра $\theta$, если для любого $\theta \in \Theta$ выполнено равенство

${\mathsf E}_\theta\, \theta^* = \theta$.

Определение 4.

Статистика $\theta^*=\theta^*(X_1, \ldots, X_n)$ называется состоятельной оценкой параметра $\theta$, если для любого $\theta \in \Theta$ имеет место сходимость

 $\theta^* \buildrel {p} \over \longrightarrow \theta$  при   $n\to\infty$.

Несмещенность — свойство оценок при фиксированном $n$. Означает это свойство отсутствие ошибки «в среднем», т.е. при систематическом использовании данной оценки.

Свойство состоятельности означает, что последовательность оценок приближается к неизвестному параметру при увеличении количества данных. Понятно, что при отсутствии этого свойства оценка совершенно «несостоятельна» как оценка.

Пример 3.

Пусть $X_1$, $\ldots$, $X_n$ — выборка объема $n$ из нормального распределения ${\mathsf N}_{a,\sigma^2}$, где $a\in {\textrm{\upshape I\kern-0.20em R}}$, $\sigma\gt$. Как найти оценки для параметров $a$ и $\sigma^2$, если оба эти параметра (можно считать это и одним двумерным параметром) неизвестны?

Мы уже знаем хорошие оценки для математического ожидания и дисперсии любого распределения.

Оценкой для истинного среднего $a={\mathsf E}\,{\!}_{a,\sigma^2}X_1$ может служить выборочное среднее $a^*=\overline X$. Свойство 2 утверждает, что эта оценка несмещенная и состоятельная.

Для дисперсии $\sigma^2={\mathsf D}\,{\!}_{a,\sigma^2}X_1$ у нас есть сразу две оценки:

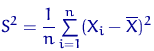  и  \begin{displaymath} S^2 = \dfrac{1}{n} \sum_{i=1}^n (X_i-\overline X)^2 \textrm{... ...и \quad} S_0^2 = \dfrac{1}{n-1}\sum_{i=1}^n (X_i-\overline X)^2\end{displaymath}

(выборочная дисперсия и несмещенная выборочная дисперсия).

Как показано в свойстве 4, обе эти оценки состоятельны, и одна из них — несмещенная.  которая? 

Следующий метод получения оценок для неизвестных параметров как раз и предлагает использовать выборочные моменты вместо истинных.


N.I.Chernova
9 сентября 2002