PREVIOUS SECTION: Stationary Sequences and Processes

1.10  On  s-algebras, generated by a sequence of r.v.'s.

(1). Let   be a probabililty space,       ,   - a sequence of r.v.'s,

  .

For  , put

(A) Remind some properties of  s-algebras.

1) If   are  s-algebras on       is  s-algebra, too, but   - not! (in general).

2) More generally, let   be any parameter set,   are  s-algebras on       is  s-algebra, too.

Therefore, is a minimal  s-algebra,  , that is    is an intersection of all s-algebras, that  .

Since   .

(B) Some properties of   :

1)   ;

2)   (triangle inequality);

Indeed,      Similarly,

3)   (since   );

4)   ;

5)   ;

Indeed,

Lemma 12

,  ,  .

Proof.  Let   be the set of events   :   ,   .

1)   . Indeed,   ,   , take

Therefore, it is sufficient to show that   is  s-algebra. Then   , and the proof is completed.

2) Prove that   is an algebra, i.e.

(i)   ;

(ii)   ;

(iii)   ,   .

(i) is obvious, (ii) follows from the property (3); (iii) follows from (5):

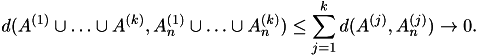
3) Prove that   is a   -algebra:

(iii')   .

Put  ,   and  .

Choose

and, for   ,

Finally, put

Then  , for  . Since   as  ,  .

QDE

Lemma 13

Let   be a double-infinite sequence of r.v.'s,   Then  .

(2). A sequence of independent r.v.'s.

Definition 10

For a sequence  , the tail  s-algebra   is

Note: Since    

Definition 11

For a sequence  ,   is right  tail  s-algebra and   is left  tail s-algebra.

Examples...

Lemma 14

If   is a sequence of independent r.v.'s, then   is trivial, i.e.

Proof.  

1)   ;

2) Since   ,   .

Therefore,

QDE

Lemma 15

If   is a sequence of independent r.v.'s, then both   and  are trivial.

NEXT SECTION: On sigma-algebras, generated by a sequence of r.v.'s., II

File translated from T_EX by T_TH, version 1.58, Htex, and with Natalia Chernova as the TeX2gif-convertor.