Lecture 1: Stopping Times - Generalization onto 2-dimensional case

PREVIOUS SECTION: Stopping Times

1.8 Generalization onto 2-dimensional case

Let and be two sequences; be a -algebra, generated by

Definition 7

A pair of r.v.'s

is a ST w.r. to

and

,

if

Lemma 7

If and are two mutually independent sequences and if is a ST, then

1) each of the sequences

is i.i.d., and they are mutually independent;

2) ; ;

3) and a random vector

are mutually independent.

Proof - omitted.

Lemma 8

In conditions of Lemma 7, assume, in addition, that

Then the sequence ,

is i.i.d.; .

Proof.

We have to show that ,

1) ,

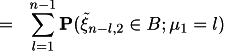2)

Problem No.6. Prove for joint distributions - by induction arguments.

QDE

Another variant of generalization on 2-dimensional case.

Lemma 9

Assume that

(i) is a sequence () of independent random vectors;

(ii) each of and is an i.i.d. sequence;

(iii) ;

(iv) is a ST and .

Then

is an i.i.d. sequence; .

Proof is very similar to that of Lemma 8 - omitted.

Finally, the last generalization (of Lemma 9).

Lemma 10

Replace in the statement of Lemma 9 (if : ...)

(i) by (i')

is an i.i.d. sequence;

and

(iv) by (iv')

is a ST,

and .

Then

is an i.i.d. sequence; .

Problem No.7. Prove Lemma 10.

NEXT SECTION: Stationary Sequences and Processes

File translated from T_EX by T_TH, version 1.58, Htex, and with Natalia Chernova as the TeX2gif-convertor.