PREVIOUS SECTION: Probabilistic Metrics

1.7  Stopping times

Let be a probability space and  be a sequence of r.v.'s, . Denote by  the -algebra, generated by :  

where =-algebra of Borel sets in .

Then, for ,  -  -algebra, generated by  ; i.e.

  is a minimal -algebra, so that  

Another way of description of  is:

  is a random vector; . Then

where  -algebra of Borel sets in .

Finally, -algebra, generated by the whole sequence .

Good Property:

For all ,   , , such that

Let now  be an integer-valued r.v.

Definition 5

Random value is called a stopping time (ST) with respect to , if  ,   (or, equivalently - ).

Another variant of definition is:

Examples ...

Assume now that  is an i.i.d. sequence,  is a ST;  . Put

Lemma 3

1)   is an i.i.d. sequence; 2)  ;  3) and a random vector   are mutually independent.

Corollary 1

and   are mutually independent.

Proof  of Lemma 3.

We have to show that   Borel sets   and   ,

Indeed,   1), 2) and 3).

First,   . Then,  

In particular,   take   and   for   . Then the l.h.s. of = the r.h.s. of =

2)

Now, take any   and replace in         by

1)

Finally, take any   and   and replace in          by       .

3)

So, let's prove  :

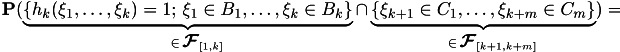
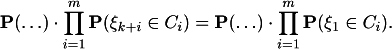
QDE

Lemma 4 (Wald identity)

Assume that   and   . Then

Proof.  

(a) Show that   .

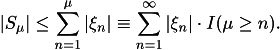
Note, that   , and  

    and   are independent     and   are independent

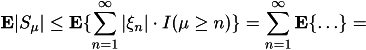
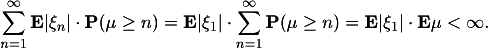
(b) Therefore,

QDE

``Induction..."

Lemma 5

Let   be an i.i.d. sequence; be a ST w.r. to  ,  ;   be as defined above;   be a ST w.r. to  ,  . Then   is a ST w.r. to  .

Proof.  

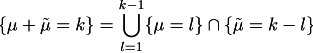
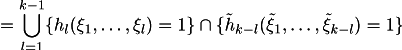
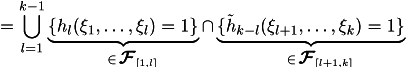
QDE

Let's write

instead of instead of . . . . . . . . .

Lemma 6

If   is a ST w.r. to     and if  , then   is a ST w.r. to  .

NEXT SECTION: Generalization onto 2-dimensional case

File translated from T_EX by T_TH, version 1.58, Htex, and with Natalia Chernova as the TeX2gif-convertor.