Совместное распределение. Независимость

Next: Моменты Up: Оглавление Previous: Функции распределения

Совместное распределение. Независимость

10.1. а) $\lim\limits_{y\to\infty}F(z,y)-F(z,z)$ ;б) $\lim\limits_{y\to\infty}F(z,y)$ ;в) $\lim\limits_{x\to\infty}F(x,z)$ .

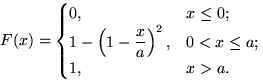
10.5. $F(x)=\begin{cases} 0, & x \le 0; \cr 1-\left(1-\dfrac{x}{a}\right)^2, & 0<x\le a; \cr 1, & x\gt a.\end{cases}$

10.6. а) Равномерное распределение на [0, 2];

б) Плотность $f(x)=\begin{cases} 0, & x \not \in [0,2]; \cr x, & 0<x\le 1; \cr 2-x, & 1<x\le 2; \end{cases}$

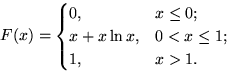
в) Функция распределения $F(x)=\begin{cases} 0, & x \le 0; \cr x+x\ln x, & 0<x\le 1; \cr 1, & x\gt 1.\end{cases}$

10.7. (а) Нет; (б, в) да.

10.8. Показать, что для , величина G(x₂,y₂)+G(x₁,y₁)- G(x₁,y₂)-G(x₂,y₁) не обязательно положительна.

10.10. $\alpha/(\alpha+\beta)$ .

10.11. а) 0; б) 1/2.

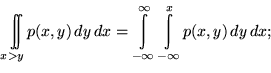
10.12. а) $\begin{displaymath} \displaystyle \iint\limits_{x\gt y}p(x,y)\,dy\,dx= \int\limits_{-\infty}^\infty\int\limits_{-\infty}^x p(x,y)\,dy\,dx;\end{displaymath}$

10.13. 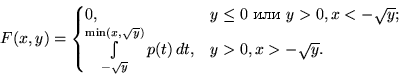$F(x,y)=\begin{cases} 0, & y \le 0 \text{ или } y\gt, x<-\sqrt{y}; \cr \int\limits_{-\sqrt{y}}^{\min(x,\sqrt{y})} p(t)\,dt, & y\gt, x\gt-\sqrt{y}.\end{cases}$

10.14. $f(x)=\begin{cases} 0, & x \not \in [0,2]; \cr 1-x/2, & 0<x\le 2.\end{cases}$

10.15. а) 1; б) $f(x)=\begin{cases} 0, & x \not \in [0,1]; \cr x+1/2, & 0<x\le 1;\end{cases}$ в) $f(x)=\begin{cases} 0, & x \not \in [0,1]; \cr 3x^2, & 0<x\le 1.\end{cases}$

10.16. б) Нет.

10.17. а), б) $f_\xi(x)=f_\eta(x)=\begin{cases} 0, & x \not \in [-1,1]; \cr 1+x, & -1<x\le 0; \cr 1-x, & 0<x\le 1; \end{cases}$ ; в) зависимы; г) некоррелированы.

10.18. 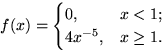$f(x)=\begin{cases} 0, & x <1; \cr 4x^{-5}, & x\ge 1.\end{cases}$

10.19. а) Нормальное распределение при a=0 , $\sigma^2=5/4$ ;б) Нормальное распределение при a=0 , $\sigma^2=1/4$ ;в) Стандартное нормальное распределение; г) $\dfrac{1}{2\pi}\,e^{-(2x^2-2xy+y^2)/2 }$ .

10.20. $f_{\xi+\eta,\xi/\eta}(x,y)=\dfrac{xe^{-x}}{(y+1)^2}$ , x , $y\ge 0$ .

10.21. а) e^-2-e^-3 ;

б) $\left(1-2\overline\Phi(1)\right)^2\approx 0{,}466$ .

10.22. ? Какой-то неправильный эллипс :)

10.23. Только если ее распределение вырождено.

10.24. Если существует $0\le x\le \pi$ такое, что $\sum\limits_{k}\mathsf P(\xi=\pi/2\pm x+2k\pi)=1$ .

10.27. Нет.

10.30. Нет.

10.31. 0, 1, 1/2.

10.32. 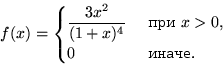$\begin{displaymath} f(x)=\begin{cases} \dfrac{3x^2}{(1+x)^4} & \text{ при } x\gt,\\ 0 & \text{ иначе.}\end{cases}\end{displaymath}$

10.34.

а) $\dfrac{p}{1+q}$ ;

б) $\dfrac{q}{1+q+q^2}$ ;

в) $\dfrac{1-p}{(2-p)^2}$ ((c) А.Н.Козырев (0125), О.И.Салмина (0136))

10.37. а) Равномерное на $[0,\,2]$ ;

б) $\xi/2+\eta$ ;

в) $\xi+\eta/2$ ;г) Функция распределения $F_{\xi\cdot\eta}(x)=0$ при $x\leq 0$ , (x+1)/2 при $0<x\leq 1$ и 1 при $x\gt 1$ ,плотность не существует (распределение не является абсолютно непрерывным); д) $\eta^\xi$ ;е) $\vert\xi-\eta\vert$ .

10.39. Распределение Пуассона с параметром $\lambda+\mu$ .

10.40. Распределение Пуассона с параметром $\lambda_1+\ldots+\lambda_n$ .

10.42. Ответ тот же, что и в задаче о встрече: 11/36.

10.43. Нормальное с параметрами a+b , $\sigma^2+\theta^2$ .

10.44. Нормальное с параметрами $\sum a_i$ , $\sum \sigma_i^2$ .

10.45. Гамма с параметрами $\alpha, \beta_1+\beta_2$ .

10.46. Гамма с параметрами $\alpha, \sum\beta_i$ .

10.47. а) Гамма с параметрами $\alpha,2$ ; б) $\dfrac{\alpha\beta}{\beta-\alpha}\left(e^{-\alpha t}-e^{-\beta t}\right)$ при $t\gt$ , 0 иначе.

10.48. Гамма с параметрами $\alpha, n$ .

10.49. Если оба распределения -- с одним и тем же параметром $\alpha$ ,то сумма имеет плотность распределения $\dfrac{\alpha\beta}{4}\,e^{\alpha\vert x\vert}(1+\alpha\vert x\vert)$ . Если параметры разные, то сумма имеет плотность распределения $\dfrac{\alpha}{4}\left(\dfrac{e^{\alpha\vert x\vert}+e^{\beta\vert x\vert}}{\al... ...eta}+ \dfrac{e^{\alpha\vert x\vert}-e^{\beta\vert x\vert}}{\beta-\alpha}\right)$ .

10.50. Если параметр масштаба у данных распределений $C_{\cdot,\sigma^2}$ один и тот же (равен $\sigma$ ), то сумма имеет распределение Коши $C_{a+b,4\sigma^2}$ с параметром сдвига a+b и параметром масштаба $2\sigma$ .

10.51. Пусть параметр масштаба у всех распределений равен 1. Сумма имеет распределение Коши с параметрами сдвига $a_1+\ldots+a_n$ и масштаба $\sigma=n$ .

10.52. а) Треугольное распределение с плотностью x при $0<x\leq 1$ , 2-x при $1< x \leq 2$ и 0 при остальных x ; б) плотность равна 0 вне отрезка $[a+c,\,b+d]$ , равна $\dfrac{1}{\max\{b-a,\,d-c\}}$ на отрезке $[\min\{b+c,a+d\},\,\max\{b+c,a+d\}]$ , линейна на каждом из отрезков $[a+c,\,\min\{b+c,a+d\}]$ и $[\max\{b+c,a+d\},\,b+d]$ .

10.53. а) $\dfrac{1}{(1+x)^2}$ при $x\gt$ ;

б) 1/2 при , $\dfrac{1}{2x^2}$ при $x\ge 1$ ;

в) стандартное распределение Коши.

10.54. а) $\dfrac{2\ln a-\ln\vert x\vert}{2a^2}$ , если $-a^2\le x\le a^2$ ; 0 иначе;

б) $\dfrac{1}{\pi}\int_0^\infty \exp\left\{-\dfrac{t^2}{2}-\dfrac{x^2}{2t^2}\right\}\cdot\dfrac{1}{t^2}\,dt$ .

10.55. а) Плотность: 1-x/2 , если $0\le x\le 2$ ; 0 иначе;

функция распределения: 0 для ; x-x²/4 для $0\le x\le 2$ ; 1 для $x\gt 2$ ;

б) функция распределения: $1-(1-F_\xi(x))\cdot(1-F_\eta(\sqrt[3]{x}))$ ;

в) функция распределения: $\dfrac{(6+x)^2}{24}$ для $-6\le x\le -4$ ; $\dfrac{x+5}{6}$ для $-4\le x\le 0$ ; $1-\dfrac{(2-x)^2}{24}$ для $0\le x\le 2$ ;

г) функция распределения: $F_\xi(x/2)\cdot F_\eta(\sqrt{x})$ ;

д) функция распределения: $F_\xi(x/3)\cdot F_\eta(\sqrt[3]{x})$ ;

е) учетверенная плотность: $\dfrac12 - \dfrac{1}{\sqrt{-x}}$ для $-4\le x\le -2$ ; $\dfrac{1}{\sqrt{2-x}}-\dfrac{1}{\sqrt{-x}}$ для $-2\le x< 0$ ; $\dfrac{1}{\sqrt{2-x}}$ для $0\le x < 2$ ; в точках разрыва -- по потребности.

10.56. а) Показательное с параметром $\alpha$ ;

б) функция распределения: $1-e^{-\alpha (x+\sqrt[3]{x})}$ ;

в) плотность распределения: $\dfrac{\alpha}{4}e^{\alpha x/3}$ для $x \le 0$ , $\dfrac{\alpha}{4}e^{-\alpha x}$ для $x\gt$ ;

г), д), е) и т.д.

10.57. а) $F(x)\cdot G(x)$ ;

б) $1-(1-F(x))\cdot(1-G(x))$ ;

в) $F(x/3)\cdot G(x)$ ;

г) $1-(1-F(x))\cdot(1-G(\sqrt[3]{x}))$ .

10.58.

а) nx^n-1 на отрезке [0,1] и 0 вне его;

б) $nC_{n-1}^kx^k(1-x)^{n-k-1}$ на отрезке [0,1] и 0 вне;

в) $n(n-1)(x^{n-2}-x^{n-1})$ на отрезке [0,1] и 0 вне;

г) $n(n-1)(y-x)^{n-2}$ при $0\le x\le y\le 1$ и 0 в остальных случаях;

д) $n(n-1)C_{n-2}^{k-1}x^{k-1}C_{n-2-k-1}^{n-m}(1-y)^{n-m}(y-x)^{m-k-1}$ при и 0 при прочих x и y .

10.59. а) 1/2;

б) показательная с параметром $2\alpha$ ;

в) 1/2.

10.60. Плотность суммы $\dfrac{1-e^{-\alpha x}}{h}$ при и $e^{-\alpha x}\dfrac{e^{\alpha h}-1}{h}$ при $x\gt h$ (ср. с ответом к 3.182 А.В.Прохоров, В.Г.Ушаков, Н.Г.Ушаков). Плотность разности $e^{-\alpha x}\dfrac{1-e^{-\alpha h}}{h}$ при $x\gt$ и $e^{-\alpha x}\dfrac{e^{\alpha x}-e^{-\alpha h}}{h}$ при $-h<x\leq 0$ .

10.61. Плотность распределения $(\xi+\eta)/\xi$ равна x^-2 при $x\geq 1$ и 0 иначе (распределение Парето); функция распределения $(\xi+\eta)/\zeta$ равна (1+x^-1)^-2 при $x\gt$ и 0 при $x\leq 0$ .

10.62. $\dfrac{\alpha^2}{3}e^{-\alpha x-\alpha y}$ при $x\geq 0$ и $y\geq 0$ , $\dfrac{\alpha^2}{3}e^{2\alpha x-\alpha y}$ при и $y\geq x$ , $\dfrac{\alpha^2}{3}e^{2\alpha y-\alpha x}$ при и $x\geq y$ .