Up: Оглавление Previous: Совместное распределение. Независимость

Моменты

11.2. а) $\mathsf E(\xi-2\eta)=0$, $\mathsf D(\xi-2\eta)=13$; б) $\mathsf E(2\xi-\eta)=3$, $\mathsf D(2\xi-\eta)=7$.

11.3. а) $np$, $npq$; б) $\lambda$, $\lambda$; в) 1/p, $q/p^2$; г) 0, $a^2/3$; д) $(a+b)/2$, $(b-a)^2/12$; е) не существуют; ж) $1/\alpha$, $1/\alpha^2$; з) 0, $2/\alpha^2$; и) $a$, $\sigma^2$.

11.4. а) 0.9, 1.29; б) 1.3, 0.41; в) 2.1, 1.49; г) 2.4, 1.99.

11.5. а) 1/6, 29/36; б), в), г) и т.д.

11.6. а) 3/4, 119/16; б), в), г) и т.д.

11.7. а) 0, 2; б) 0, 2; в) 1.2, 0.56; г) 2, 2.8.

11.8. а) $\dfrac{1-e^{-\lambda}}{\lambda}$; б) $\dfrac{1-q^{n+1}}{p(n+1)}$.

11.9. а) $\dfrac{e^{-\lambda}+\lambda-1}{\lambda^2}$.

11.10. $V=a(\xi+0.5)$, где $\xi$ имеет геометрическое с параметром $p=(1-e^{-ab})$распределение, ${\mathsf E}V=a\cdot\left(p^{-1}+0.5\right)$ и ${\mathsf E}V^2=a^2\left(2p^{-2}+0.25\right)$.

11.13. а) Распределение симметрично, $\mathsf P(\xi=-2)=1/24, \mathsf P(\xi=-1)=1/3$; б) распределение симметрично, $\mathsf P(\xi=-2)=1/6, \mathsf P(\xi=-1)=1/3$.

11.14. Нет.

11.15. а) 2/3, 1/18; б) 1/4, 1/12-1/16; в) 1/2, 1/12; г) $\mathsf E 2^\xi=\dfrac{4}{\ln 2}-\dfrac{2}{(\ln 2)^2}$, $\mathsf E 2^{2\xi}=\dfrac{4}{\ln 2}-\dfrac{3}{2(\ln 2)^2}$.

11.16. Функция $p(x)$ не является плотностью. Поправить и посчитать самим.

11.17. 1/2, 1/8.

11.18. $(\ln 2)/\pi -0.5$.

11.19. Математическое ожидание -- при $\alpha \gt 1$, дисперсия -- при $\alpha \gt 2$.

11.20. $\dfrac{\pi(b^3-a^3)}{12(b-a)}$.

11.21. а) $\sqrt{2/\pi}$; б) $\mathsf E\xi^{2n+1}=0$, $\mathsf E\xi^{2n}=(2n-1)!!$

11.22. $\sigma\sqrt{2/\pi}$;

11.23. 0, 3.

11.24. а) 4; б) 4; в) 4.5; г) -10/3; д) 11/6; е) 11/6.

11.25. а) 1/12, 3/4-1/144; б) 0, 1; в) -1/4; г) 1/12, 5.75-1/144.

11.26. Аналогично

11.27. Аналогично

11.28. ${\mathsf E}\xi=4/3$, ${\mathsf E}\eta=1/3$, ${\mathsf D}\xi=2/9$,${\mathsf D}\eta=1/18$, ${\bf Cov}(\xi,\eta)=1/18$ (если верно, что $\mathsf E(\xi\eta)=1/2$). Зависимы: например, $\mathsf P(\xi<1, \eta\gt.5)=0\neq 1/16$.

11.29. ${\mathsf E}\xi={\mathsf E}\eta=0$, ${\bf Cov}(\xi,\eta)=0$. Зависимы.

11.30. $\mathsf E\xi\eta=0$, ${\bf Cov}(\xi,\eta)=0$. Зависимы.

11.31. а) 1/4, 1/9-1/16; б) 2/3, 1/18.

11.32. б) 1.5, 1/12.

11.33. ${\mathsf E}\xi={\mathsf E}\eta=7/12$, ${\mathsf D}\xi={\mathsf D}\eta=11/144$,${\bf Cov}(\xi,\eta)=1/3-49/144$.

11.38. Распределение Коши.

11.39. Распределение Парето с плотностью $f_\xi(x)=\dfrac{c}{x^3}$ при $x\gt 1$.

11.47. Не обязательно.

11.50. $\xi=\eta=\sqrt{\zeta}$, $\zeta$ имеет распределение Коши.

11.51. $\mathsf D\xi$.

11.52. Медиана распределения $\xi$.

11.55. $3.5n$, $35n/12$.

11.56. $365\cdot\left(\dfrac{364}{365}\right)^n$, $365\cdot 364\cdot\left(\dfrac{363}{365}\right)^n+365\cdot\left(\dfrac{364}{365}\right)^n\left(1-365\cdot\left(\dfrac{364}{365}\right)^n\right)$.
Указание. Число есть сумма единиц. Поэтому число дней, на которые не приходится ни одного д.р., есть сумма (по всем дням года) индикаторов того, что на данный день не приходится ни одного д.р. из $n$.Поэтому $\xi=\xi_1+\dots+\xi_{365}$, где $\xi_i=1$ с вероятностью $(364/365)^n$и $\xi_i=0$ с вероятностью $1-(364/365)^n$. Слагаемые зависимы, и $\xi_i\cdot\xi_j$при $i\neq j$ также имеет распределение Бернулли с параметром $p=(363/365)^n$.

11.57. $365 C_{365}^k\cdot (365)^{-k}\left(\dfrac{364}{365}\right)^{n-k}$,

11.58. $365-365\cdot\left(\dfrac{364}{365}\right)^n- 365 \left(\dfrac{364}{365}\right)^{n-1}$.

11.59. $\mathsf E\vert\xi_1-\xi_2\vert=a/3$, $\mathsf E\vert\xi_1-\xi_2\vert=a^2/18$, $\mathbf{Cov}(\min\{\xi_1,\xi_2\},\max\{\xi_1,\xi_2\})=a^2/36$.

11.60. Вообще говоря, нет.

11.62. а) $np^2$, $np^2(1-p^2)+2(n-1)(p^3-p^4)$; б) $np^3$, $np^3(1-p^3)+2(n-1)(p^4-p^6)+2(n-2)(p^5-p^6)$; в) аналогично.

11.63. $\mathsf E\xi=1$, $\mathsf D\xi=1$. См. указание к задаче 11.56.

11.64. –1/5.

11.65. $n(1-1/n)^r$.

11.66. $k\cdot\dfrac{a}{a+b}$, $k\cdot\dfrac{a}{a+b}\left(1-\dfrac{a}{a+b}\right)\cdot\dfrac{a+b-k}{a+b-1}$.

11.67. $\xi$ и $\xi^2$, где $\xi$ имеет стандартное нормальное распределение.

11.69. $1/\sqrt{10}$.

11.70. а) $-1/\sqrt{e-1}$; б) аналогично.

11.73. 0.

11.74. а) Нет, б) да.

11.75. $(n-m)/n$.

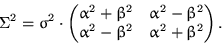
11.76. $\rho=\dfrac{\alpha^2-\beta^2}{\alpha^2+\beta^2}$; нормальное с вектором средних $(a(\alpha+\beta),a(\alpha-\beta)$ и матрицей ковариаций \begin{displaymath} \Sigma^2=\sigma^2\cdot \begin{pmatrix} \alpha^2+\beta^2 & \a... ...\beta^2 \cr \alpha^2-\beta^2 & \alpha^2+\beta^2 \end{pmatrix}.\end{displaymath}

11.77. Бернулли. Ищите еще.

11.78. Бернулли. Ищите еще.

11.80. Удовлетворяющих равенству $\rho=\dfrac{a+b}{1+ab}$.

11.81. 0.

11.83. $ab$, $\sigma^2 b+a^2\theta^2$.

11.84. $e$.

11.86. $1-J(1-1/J)^n$, или я не понимаю условие.

11.89. Неравенство в п.б) неверно.

11.94. Нет, если скорость не постоянна.


N.I.Chernova
4/19/2003