Next: Совместное распределение. Независимость Up: Оглавление Previous: Случайные величины

Функции распределения

9.1. a)

$x_i$ 5 2 1
${\bf P}\{\xi^2+1=x_i\}$ 2/10 1/2 3/10
.

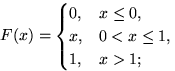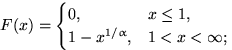
9.4. а), д) $F(x)=\begin{cases} 0, & x\le 0,\cr x, & 0<x\le 1, \cr 1, & x\gt 1;\end{cases}$ б) $F(x)=\begin{cases} 0, & x\le 1,\cr 1-x^{1/\alpha}, & 1<x< \infty;\end{cases}$

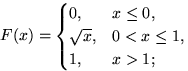в) $F(x)=\begin{cases} 0, & x\le 0,\cr \sqrt{x}, & 0<x\le 1, \cr 1, & x\gt 1;\end{cases}$ г) $F(x)=\begin{cases} 0, & x\le 0,\cr \dfrac2\pi\textrm{arcsin}(x), & 0<x\le 1, \cr 1, & x\gt 1;\end{cases}$

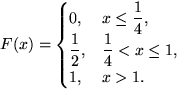
е) $F(x)=\begin{cases} 0, & x \le -1,\cr \dfrac43+\sqrt[3]{x}, & -1<x\le -\dfrac{8}... ...\dfrac{8}{27}<x\le 0,\\ [1ex] \dfrac23+x, & 0<x\le 1,\cr 1, & x\gt 1;\end{cases}$ ж) $F(x)=\begin{cases} 0, & x \le \dfrac14,\cr \dfrac12, & \dfrac14<x\le 1, \\ 1, & x\gt 1.\end{cases}$

9.5. Не существуют в е), ж).

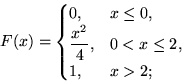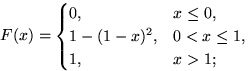9.6. а) $F(x)=\begin{cases} 0, & x\le 0,\cr \dfrac{x^2}{4}, & 0<x\le 2, \cr 1, & x\gt 2;\end{cases}$ б) $F(x)=\begin{cases} 0, & x\le 0,\cr 1-(1-x)^2, & 0<x\le 1, \cr 1, & x\gt 1;\end{cases}$.

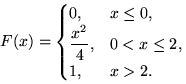
9.7. а) $F(x)=\begin{cases} 0, & x\le 0,\cr \dfrac{2}{\pi}\textrm{arcsin}(x/2), & 0<x\le 2, \cr 1, & x\gt 2;\end{cases}$ б) $F(x)=\begin{cases} 0, & x\le 0,\cr \dfrac{x^2}{4}, & 0<x\le 2, \cr 1, & x\gt 2.\end{cases}$

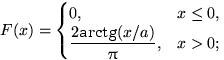9.8. а) $F(x)=\begin{cases} 0, & x\le 0,\cr \dfrac{2\textrm{arctg}(x/a)}{\pi}, & x\gt;\end{cases}$ б) $F(x)=\dfrac{ \textrm{arctg}(x/a) }{\pi}+\dfrac{1}{2}$.

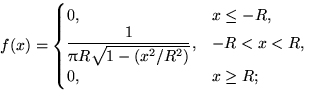
9.9. а) $f(x)=\begin{cases} 0, & x\le -R,\cr \dfrac{1}{\pi R \sqrt{1-(x^2/R^2)}}, & -R<x< R, \cr 0, & x\ge R; \end{cases}$

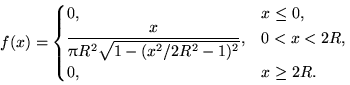
б) $f(x)=\begin{cases} 0, & x\le 0,\cr \dfrac{x}{\pi R^2 \sqrt{1-(x^2/2R^2-1)^2}}, & 0<x < 2R, \cr 0, & x\ge 2R. \end{cases}$

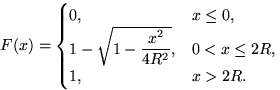
9.10. $F(x)=\begin{cases} 0, & x\le 0,\cr 1-\sqrt{1-\dfrac{x^2}{4R^2}}, & 0<x\le 2R, \cr 1, & x\gt 2R.\end{cases}$

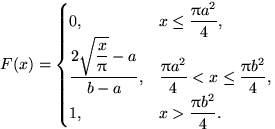
9.11. $F(x)=\begin{cases} 0, & x\le \dfrac{\pi a^2}{4},\cr \dfrac{2\sqrt{\dfrac{x}{\pi... ...pi a^2}{4}<x\le \dfrac{\pi b^2}{4}, \cr 1, & x\gt\dfrac{\pi b^2}{4}.\end{cases}$

9.12. $\alpha$.

9.13. $\dfrac{1}{\pi}$.

9.14. $\dfrac{\alpha^{\beta+1}}{\Gamma(\beta+1)}$.

9.15. $\dfrac{2}{\pi}$.

9.16. а), в) Да; б), г) Нет.

9.17. а), г) Показательное с параметром 1;

б) Равномерное на [1,3];

д) 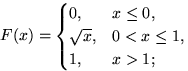$F(x)=\begin{cases} 0, & x\le 0,\cr \sqrt{x}, & 0<x\le 1, \cr 1, & x\gt 1;\end{cases}$.

9.18. а) 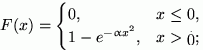$F(x)=\begin{cases} 0, & x\le 0,\cr 1- e^{-\alpha x^2}, & x\gt 1;\end{cases}$

б) 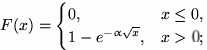$F(x)=\begin{cases} 0, & x\le 0,\cr 1- e^{-\alpha \sqrt{x}}, & x\gt 1;\end{cases}$ в) Показательное с параметром $\alpha/2$;

г) $F(x)=1- e^{-e^x}$;

д) Равномерное на [0,1]; е) 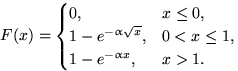$F(x)=\begin{cases} 0, & x\le 0,\cr 1- e^{-\alpha \sqrt{x}}, & 0<x\le 1, \cr 1-e^{-\alpha x}, & x\gt 1.\end{cases}$

9.20. $f(x)=\dfrac{1}{x\sqrt{2\pi}}\exp\left\{{-\dfrac12\ln^2 x}\right\}$.

9.21. Стандартное распределение Коши.

9.22. а) $\dfrac{1}{\vert a\vert}p\left(\dfrac{x-b}{a}\right)$; б) $\dfrac{1}{x^2}p\left(\dfrac{1}{x}\right)$;

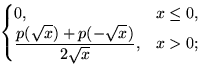в) $\begin{cases} 0, & x\le 0, \cr \dfrac{p(\sqrt{x})+p(-\sqrt{x})}{2\sqrt{x}}, & x\gt;\end{cases}$;

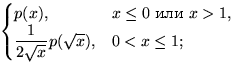
г) $\begin{cases} p(x), & x\le 0 \text{ или } x\gt 1, \cr \dfrac{1}{2\sqrt{x}}p(\sqrt{x}), & 0<x\le 1;\end{cases}$

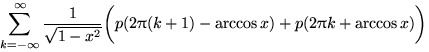д) $\displaystyle\sum\limits_{k=-\infty}^{\infty}\dfrac{1}{\sqrt{1-x^2}}\biggl(p(2\pi(k+1)-\arccos x)+p(2\pi k+\arccos x)\biggr)$, если $-1<x<1$ и 0 для остальных $x$;

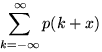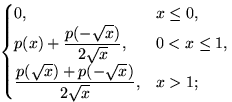
е) $\displaystyle\sum\limits_{k=-\infty}^{\infty}p(k+x)$, если $0<x<1$ и 0 для остальных $x$; ж) $p(x+1)+p(-x+1)$; з) $\begin{cases} 0, & x\le 0, \cr p(x) + \dfrac{p(-\sqrt{x})}{2\sqrt{x}}, & 0<x\le 1, \cr \dfrac{p(\sqrt{x})+p(-\sqrt{x})}{2\sqrt{x}}, & x\gt 1;\end{cases}$

9.26. Показательное распределение с параметром 1.

9.27. Не скажу.

9.28. $F(\sqrt[s]{x})-F(-\sqrt[s](x))$.

9.29. $\mathsf P(\eta=-1)=F(0)=1-\mathsf P(\eta=1)$, непрерывность в нуле ни при чем.

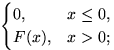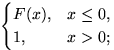9.30. a), в) $\begin{cases} 0, & x\le 0, \cr F(x), & x\gt;\end{cases}$б) $\begin{cases} F(x), & x\le 0, \cr 1, & x\gt;\end{cases}$ г) $1-F((2-x)/3+0)$.


N.I.Chernova
3/18/2002