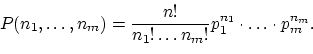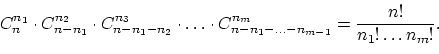Независимые испытания с несколькими исходами

Рассмотрим следующий пример, когда из двух очень похожих вопросов на один можно ответить, пользуясь формулой Бернулли, а для другого этой формулы оказывается недостаточно.

Пример 24. Игральная кость подбрасывается пятнадцать раз. Найти вероятности следующих событий: а) выпадет ровно десять троек; б) выпадет ровно десять троек и три единицы.

Решение.

а) Есть пятнадцать испытаний схемы Бернулли с вероятностью успеха 1/6 (здесь успех — выпадение тройки). Вероятность десяти успехов в пятнадцати испытаниях равна

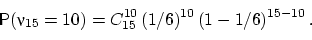
б) Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение остальных граней. Воспользоваться формулой для числа успехов в схеме Бернулли не удаётся — перед нами уже не схема Бернулли.

Осталось изобрести формулу для подсчёта вероятности каждому исходу в нескольких независимых испытаниях выпасть нужное число раз, если в одном испытании возможно не два, а более исходов.

Пусть в одном испытании возможны исходов: , и исход в одном испытании случается с вероятностью , где . Обозначим через искомую вероятность того, что в независимых испытаниях исход 1 появился раз, исход 2 — раз, и т.д., исход — раз.

Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению

единиц,

двоек, ...,

раз

-ок:

Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданом порядке. Вероятность такого результата независимых испытаний равна .

Остальные благоприятные исходы отличаются лишь расположением чисел на местах. Число таких исходов равно числу способов расставить на местах единиц, двоек, ..., чисел , т.е.

QED

Теперь мы можем вернуться к примеру 24(б) и выписать ответ: так как вероятности выпадения тройки и единицы равны по 1/6, а вероятность третьего исхода (выпали любые другие грани) равна 4/6, то вероятность получить десять троек, три единицы и ещё два других очка равна

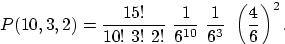
§ 3. Независимые испытания с несколькими исходами