Пример 16 (нерегулярное семейство).
Рассмотрим «смещенное»
показательное распределение с параметром сдвига 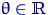 и
плотностью
и
плотностью
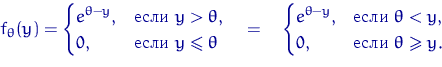
Поскольку при любом  распределение сосредоточено на
распределение сосредоточено на  , а параметр
, а параметр  может принимать любые вещественные значения,
то только
может принимать любые вещественные значения,
то только 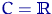 (плюс-минус множество меры нуль)
таково, что при любом
(плюс-минус множество меры нуль)
таково, что при любом  выполнено
выполнено
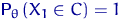 . Покажем, что условие (R)
опять не выполнено:
множество тех
. Покажем, что условие (R)
опять не выполнено:
множество тех 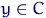 , при каждом из которых функция
, при каждом из которых функция  дифференцируема по
дифференцируема по  , столь же пусто, как и в примере 15.
, столь же пусто, как и в примере 15.
Рис. 6:
Пример 16
|
![\begin{figure}
\unitlength=.8mm
\linethickness {0.5pt}
\begin{picture}
(65.00...
...cc]{$y$}}
\put(65.00,1.00){\makebox(0,0)[cc]{$\theta$}}\end{picture}\end{figure}](img570.gif)
|
При фиксированном 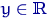 на рисунке 6 изображена
функция
на рисунке 6 изображена
функция 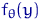 (а может быть, корень из нее)
как функция переменной
(а может быть, корень из нее)
как функция переменной  .
.
Какое бы 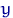 ни было,
ни было, 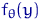 даже не является
непрерывной по
даже не является
непрерывной по  , а тем более дифференцируемой.
, а тем более дифференцируемой.
![]() с параметром
с параметром ![]() . Плотность этого распределения имеет вид
. Плотность этого распределения имеет вид
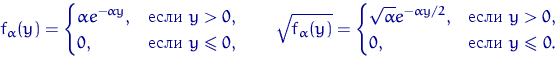
![]() можно взять
можно взять ![]() , поскольку
, поскольку ![]() .
При любом
.
При любом ![]() , т.е. при
, т.е. при ![]() , существует производная функции
, существует производная функции ![]() по
по ![]() , и эта производная непрерывна во всех точках
, и эта производная непрерывна во всех точках ![]() :
:
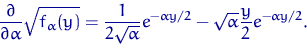
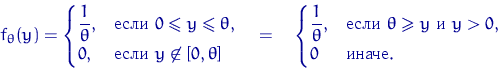
![\begin{figure}
% latex2html id marker 2232
\unitlength=.8mm
\linethickness {0....
...(3,4.5){
\reflectbox {\includegraphics[scale=1]{plo}}
}\end{picture}\end{figure}](img566.gif)
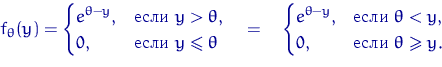
![\begin{figure}
\unitlength=.8mm
\linethickness {0.5pt}
\begin{picture}
(65.00...
...cc]{$y$}}
\put(65.00,1.00){\makebox(0,0)[cc]{$\theta$}}\end{picture}\end{figure}](img570.gif)