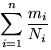 .
.7.1. Равновероятно.
7.2. ![]()
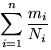 .
.
7.3. 0,4.
7.4. 0,52.
7.5. а) 2 белых и 3 черных шара; б) ![]() .
.
7.6. а) 1.
б) ![]() .в)
.в) 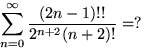 , где
, где ![]() .
.
7.7. ![]() .
.
7.8. ![]() .
.
7.9. ![]() ,
, ![]() .
.
7.10. ![]() .
.
7.11. 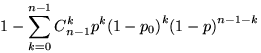 .
.
7.12. ![]() .
.
7.13. ![]() .
.
7.14. Вероятнее, что ![]() попал в мишень.
попал в мишень.
7.15. 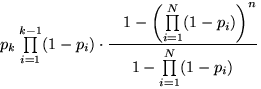 .
.
7.16. ![]() .
.
7.17. а) ![]() ; б)
; б) ![]() .
.
7.18. ![]() .
.
7.19. ![]() .
.
7.20. ![]() .
.
7.21. ![]() .
Указание. Здравый смысл подсказывает, что под геометрическим распределением
в условии понимается распределение числа неудач до первого успеха:
.
Указание. Здравый смысл подсказывает, что под геометрическим распределением
в условии понимается распределение числа неудач до первого успеха:
![]() Ответ приведен для этого условия.
В любом случае следует воспользоваться равенством
Ответ приведен для этого условия.
В любом случае следует воспользоваться равенством
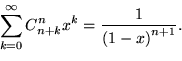
7.22. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
7.23. а) 1/132; б) 1/12.
7.24. ![]() .
.
7.25. 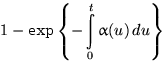 .
.
7.26. Для ![]()
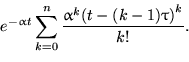
7.27. ![]() .
.
7.28. ![]() .
.
7.29.
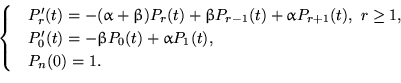
7.30. ![]() .
.
7.31. ![]() .
.
7.32. Та же самая.
7.33. ![]() .
.
7.34. ![]() ;
; ![]() .
.
7.35. 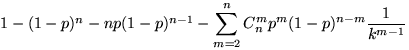 .
.
7.36. "Какая гадость эта ваша заливная рыба..."
7.37. 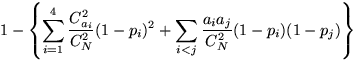 .
.
7.38. ![]() .
.
7.39. Лениво.
7.40. ![]() .
.
7.41.  ;
; 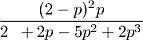 .
.
7.42. а) ![]() ; б)
; б) ![]() ; здесь
; здесь ![]() .
.