Несколько слов о геометрически самоподобных фракталах

Предлагаемые Вашему вниманию картинки есть стилизованные изображения двупорожденных геометрически самоподобных фракталов - инвариантных множеств пары линейных отображений плоскости. Заметим сразу, что данный класс множеств есть лишь малая часть всего класса фрактальных множеств (то есть множеств дробной хаусдорфовой размерности).

Фракталы изучают все, кому не лень - и физики, и математики, и химики, и компьютерщики. По большому счету, все сложные системы обладают теми или иными свойствами самоподобия, что позволяет изучать эти системы, не анализируя каждый элемент в отдельности, а лишь зная законы взаимосвязи элементов системы. Заметим, что точно то же самое (с заменой слова "самоподобие" на слово "случайность") часто говорится в объяснение широкого распространения вероятностных методов. Неудивительно, что и в исследовании (геометрически самоподобных) фракталов часто используют теорию случайных процессов и прочие сугубо вероятностные вещи.

Опишем вкратце, что такое двупорожденные геометрически самоподобные фракталы. Рассмотрим два линейных отображения комплексной плоскости:   и  где  - комплексные числа и   У каждого из этих отображений есть неподвижная точка. Эти точки   и   находятся из уравнений    Геометрический смысл отображения  - композиция сжатия с коэффициентом   и поворота на угол   относительно неподвижной точки   Аналогичный смысл имеет отображение   Инвариантным множеством системы отображений называется компактное множество   такое, что   Такое множество может иметь дробную (fractal) хаусдорфову размерность и быть достаточно сложно устроено. Замечательно, что с точностью до размера, это множество полностью определяется числами   то есть всего лишь восемью действительными числами.

Наиболее простая (но не наиболее эффективная) схема построения инвариантного множества такова: положим 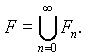  и т.д. Тогда