Распределение Стьюдента и его свойства

Next: Распределение Фишера Up: Распределения, связанные с нормальным Previous: Распределение «хи-квадрат»

6.3. Распределение Стьюдента и его свойства

Определение 17.

Пусть $\xi_0$ , $\xi_1$ , $\ldots$ , $\xi_k$ независимы и имеют стандартное нормальное распределение. Распределение случайной величины

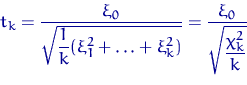
$\begin{displaymath} t_k=\dfrac{\xi_0}{\sqrt{\dfrac{1}{k}(\xi_1^2+\ldots+\xi_k^2)}}= \dfrac{\xi_0}{\sqrt{ \dfrac{\chi^2_k}{k}}}\end{displaymath}$

называют распределением Стьюдента с степенями свободы и обозначают ${\mathsf T}_k$ .

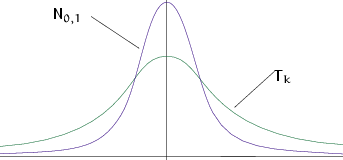$\begin{figure}...\end{figure}$ Плотность распределения Стьюдента по сравнению с плотностью стандартного нормального распределения.

Плотность распределения Стьюдента с степенями свободы равна разглядеть как следует!

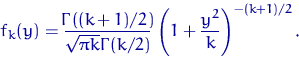$\begin{equation} f_k(y)=\dfrac{\Gamma(k+1)/2}{\sqrt{\pi k}\Gamma(k/2)}\,\left(1+\dfrac{y^2}{k}\right)^{-(k+1)/2}.\end{equation}$ (15)

Мы не станем выводить эту формулу, предложив читателю-математику либо вывести ее самостоятельно, либо посмотреть вывод в [1, п. 6-7 §2 главы 2].

Свойства распределения Стьюдента:

1.: Симметричность.
Если случайная величина имеет распределение Стьюдента ${\mathsf T}_k$ с степенями свободы, то и имеет такое же распределение.
Упражнение. Доказать.
2.: Асимптотическая нормальность.
Распределение Стьюдента ${\mathsf T}_k$ слабо сходится к стандартному нормальному распределению при $k\to\infty$ .
Доказательство. Пусть $\xi_0$ , $\xi_1$ , $\ldots$ , $\xi_k$ независимы и имеют стандартное нормальное распределение. Тогда ${\mathsf E}\,\xi_1^2=1$ , и по ЗБЧ
$\begin{displaymath} \dfrac{\chi^2_k}{k}=\dfrac{\xi_1^2+\ldots+\xi_k^2}{k} \buildrel {p} \over \longrightarrow 1 \end{displaymath}$ при $k\to\infty$ .
Тогда и
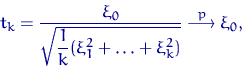
$\begin{displaymath} t_k=\dfrac{\xi_0}{\sqrt{\dfrac{1}{k}(\xi_1^2+\ldots+\xi_k^2)}} \buildrel {p} \over \longrightarrow \xi_0,\end{displaymath}$
откуда следует и слабая сходимость последовательности случайных величин с распределением Стьюдента к $\xi_0$ , имеющей стандартное нормальное распределение. То есть ${\mathsf T}_k\Rightarrow{\mathsf N}_{0,1}$ .
Q.D.E.
3.: Распределение Стьюдента с одной степенью свободы есть стандартное распределение Коши.
Упражнение. Как получить случайную величину с распределением Коши, имея две независимые стандартные нормальные случайные величины?

Доказательство. Подставим в плотность (15), используя $\Gamma(1/2)=\sqrt{\pi}$ и $\Gamma(1)=1$ , и получим плотность распределения Коши:
$\begin{displaymath} f_1(y)=\dfrac{1}{\pi}\,\left(1+y^2\right)^{-1}\end{displaymath}$ .
Q.D.E.
4.: У распределения Стьюдента существуют только моменты порядка , и не существуют моменты порядка $m\geqslant k$ . При этом все существующие моменты нечетного порядка равны нулю.
Упражнение. Посмотреть на плотность (15) и убедиться в сходимости или расходимости на бесконечности при соответствующих интегралов
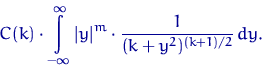
$\begin{displaymath} C(k)\cdot \int\limits_{-\infty}^\infty {\lvert y \rvert}^m \cdot \dfrac{1}{(k+y^2)^{(k+1)/2}}\,dy.\end{displaymath}$

Отметим, что и распределение $\chi^2$ , и распределение Стьюдента табулированы, так что если в каких-то доверительных интервалах появятся квантили этих распределений, то мы найдем их по таблице. Следущее распределение тоже тесно связано с нормальным распределением, но понадобится нам не при построения доверительных интервалов, а чуть позже — в задачах проверки гипотез. Там же мы поймем, почему его называют часто распределением дисперсионного отношения. Призываем математиков сравнить определение [1, п. 6 § 2 гл. 2] с нашим определением и учесть, что в статистических таблицах всегда табулируется распределение Фишера в том виде, как мы его сейчас определим. что было раньше - курица или яйцо?

N.I.Chernova 9 сентября 2002