PREVIOUS SECTION: Properties of UI

1.5  Coupling inequality. Maximal coupling. Dobrushin's theorem

In this section, we assume that random variables are not necessary real-valued, but may take values in some measurable space  that is assumed to be complete separable metric space.

Coupling inequality

Let   be two  -valued r.v.'s.

Put  

Then, for ,  

Therefore, for any , , that is

Maximal coupling

Let's reformulate the statement. Note that l.h.s. of inequality (*) depends on "marginal" distributions  and  only and does not depend on the joint distribution of  and . Therefore, we get the following:

for given  and  and for any their coupling (*) takes place. Or, equivalently,

(?) May be, in  is equality?

(??) If "yes", then does there exists such a coupling that

Both answers are positive! And this is the statement of Dobrushin's theorem.

Proof.   is a signed measure. Therefore, Banach theorem states that

there exists a subset :

(a)    ;

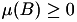
(b) .

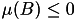
Note:

1) if , then  and the coupling is obvious;

2) .

Assume . Introduce 4 distributions (probability measures):

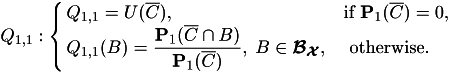
Similarly,

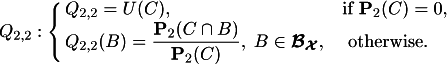
Then, define 5 independent r.v.'s:   and

	1	2	0

Now we can "construct"  and :  

Simple calculations show that , .

Then,  

So,  

and the proof is completed.

QDE

NEXT SECTION: Probabilistic Metrics

File translated from T_EX by T_TH, version 1.58, Htex, and with Natalia Chernova as the TeX2gif-convertor.