Lecture 1: Uniform Integrability

PREVIOUS SECTION: Introduction, Convergences

1.3 Uniform integrability

Let be a sequence of real-valued r.v.'s.

Definition 1

R.v.'s are uniformly integrable (UI), if and, moreover,

We can assume the upper bound to be monotone and right-continuous.

Lemma 1

The following are equivalent:

(i) are UI;

(ii) a function :

(a) ; ; ;

(b)

Note: is not essential!

Proof.

(ii) (i). For each ,

From (i) to (ii). Assume that (otherwise, the statement is trivial).

For , put

and, for , put . From get .

Note: is an interval, and if is its left boundary point, then . Therefore,

Remark 1

As a corollary, one can get the following:

if , then from Lemma 1 such that .

"If the first moment" " something more".

Lemma 2

Assume . Then holds

(1) are UI and ;

(2) ; ; are UI.

Remark 2. In (2), the condition may be weakened in a natural way.

Problem No.2. How?

But it cannot be eliminated.

Example.

			0

, but are not UI!

Proof of Lemma 2.

First, note that both statements (1) and (2) are "marginal", i.e. only marginal distributions are involved. So, we can construct a coupling: .

Prove (1).

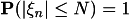
(a) Assume that : (this is a special case of UI).

Then and, ,

Therefore, .

(b) Assume now that and for some .

Since , then

Then, and

(c) Prove: . Indeed,

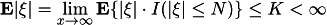
(d) , choose : and .

Then,

Since and , then

and for any

QDE

Prove (2).

Use (b) from the proof of (1): for a given ,

Therefore, :

Now,

Set . Then

Therefore,

QDE

NEXT SECTION: Properties of UI

File translated from T_EX by T_TH, version 1.58, Htex and with Natalia Chernova as the TeX2gif-convertor.