- 1.
- В урне 12 белых и 3 черных шара. Вася и Петя по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [1, 3] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 0.
- 3.
- Студент Вася Иванов может попасть домой
по любому из двух темных переулков. И в том, и в другом переулке
по 6 фонарей, для каждого из которых, независимо от других, равновозможно
— гореть или нет. Вася войдет в переулок только если в нем горит
хотя бы два фонаря.
а) С какой вероятностью Вася попадет домой?
б) С какой вероятностью оба переулка будут достаточно освещены,
так что Вася очень долго будет выбирать нужный переулок?
- 4.
- У Пети в левом кармане — 10 монет по 1 коп. и 3 монеты
по 5 коп., а в правом кармане — 4 монеты по 1 коп. и 8 монет по 5 коп.
Петя достает из наудачу выбранного кармана 3 монеты. Найти вероятность
того что:
а) все три монеты — по 1 коп.;
б) ровно две из трех монет — по 1 коп.;
в) Петя выбрал левый карман, если все 3 монеты оказались по 1 коп.
- 5.
- Событие
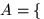 хотя бы один из трех проверяемых утюгов
неисправен}, событие
хотя бы один из трех проверяемых утюгов
неисправен}, событие 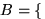 все три утюга исправны}. Что означает
событие
а)
все три утюга исправны}. Что означает
событие
а) 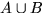 ; б)
; б) 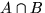 ;
в)
;
в) 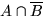 ; г)
; г) 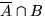 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 11 белых и 4 черных шара. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [0, 2] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 1.
- 3.
- Чтобы не проспать лекцию по теории вероятностей,
живущие в соседних комнатах Вася Иванов и Коля Петров ставят
перед собой на одно и то же время по 5 будильников каждый. Любой из этих
будильников утром звенит либо не звенит с равной вероятностью.
Для того, чтобы любой из друзей проснулся,
требуется звон не менее двух будильников. Проснувшийся
немедленно бежит разбудить товарища.
а) С какой вероятностью друзья придут на лекцию?
б) С какой вероятностью они столкнутся в коридоре при попытке
разбудить друг друга?
- 4.
- У Васи в левом кармане — 9 жевательных резинок
«Dirol» и 4 «Orbit», а в правом — 4 «Dirol»
и 8 «Orbit».
Вася достает из наудачу выбранного кармана 3 жевательных резинки.
Найти вероятность того что:
а) все три — «Dirol»;
б) ровно две из трех — «Dirol»;
в) Вася выбрал левый карман, если все 3 резинки оказались «Dirol».
- 5.
- Событие
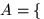 все 11 рек на карте текут на север}, событие
все 11 рек на карте текут на север}, событие 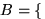 хотя бы одна из 11 рек не течет на север}. Что означает событие
а)
хотя бы одна из 11 рек не течет на север}. Что означает событие
а) 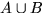 ; б)
; б) 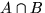 ;
в)
;
в) 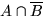 ; г)
; г) 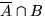 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 10 белых и 5 черных шаров. Вася и Петя по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [2, 4] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 2.
- 3.
- На доске объявлений ЭФ висят два листка для записи
на спецкурсы. У каждого листка в полном недоумении стоят по 4 студента.
Первые четверо думают, с одной «м» или с двумя пишется слово
«имитация». Еще четверо гадают, не добавить ли букву «ф»
в слово «офис». В итоге каждый принимает решение наудачу
и независимо от остальных («правильно» или «нет» с вероятностью 1/2).
На листке делаются исправления, если хотя
бы двое из 4 стоящих около него студентов решили,
что слово написано неверно.
а) С какой вероятностью хоть одно из слов окажется «исправленным»?
б) С какой вероятностью студенты «исправят» оба слова?
- 4.
- Перед Колей — 2 колоды карт. В левой колоде 10 красных
и 3 черных, а в правой — 3 красных и 9 черных.
Коля закрывает глаза и из наудачу выбранной колоды карт
достает 3 карты. Найти вероятность того что:
а) все три карты красные;
б) ровно две из трех карт красные;
в) Коля выбрал левую колоду, если все 3 карты оказались красными.
- 5.
- Событие
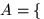 хотя бы одна из 4 страниц содержит
опечатки}, событие
хотя бы одна из 4 страниц содержит
опечатки}, событие 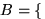 все 4 страницы без опечаток}. Что означает событие
а)
все 4 страницы без опечаток}. Что означает событие
а) 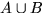 ; б)
; б) 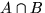 ;
в)
;
в) 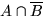 ; г)
; г) 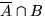 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 9 белых и 6 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [0, 2] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 3.
- 3.
- Живущие в разных комнатах (в противоположных концах)
общежития Вася Иванов и Коля Петров проводят эксперимент,
бросая, каждый из своего окна,
пакеты с водой на проходящих под окном друзей. Всего у Васи и Коли
по 7 пакетов с водой. Каждый вовлеченный в эксперимент с равной
вероятностью возвращается либо к себе в комнату, либо в комнату
к экспериментатору. Для того, чтобы открыть крепкую дверь в комнату,
нужны по крайней мере двое очень рассерженных друзей.
а) С какой вероятностью в общежитии станет меньше целых дверей?
б) С какой вероятностью целых дверей станет меньше на две?
- 4.
- В первом ящике — 9 старых и 4 новых теннисных мяча,
а во втором — 3 старых и 9 новых.
Вася достает 3 мяча из наудачу выбранного ящика.
Найти вероятность того что:
а) все три мяча новые;
б) ровно два из трех мячей новые;
в) Вася выбрал первый ящик, если все 3 мяча оказались новыми.
- 5.
- Событие
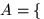 все 9 лампочек в люстре горят}, событие
все 9 лампочек в люстре горят}, событие 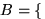 хотя бы одна из 9 лампочек не горит}. Что означает событие
а)
хотя бы одна из 9 лампочек не горит}. Что означает событие
а) 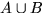 ; б)
; б) 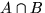 ;
в)
;
в) 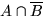 ; г)
; г) 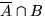 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 8 белых и 7 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [1, 3] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 4.
- 3.
- Студенты Вася Иванов и Коля Петров раскладывают
на противоположных лестницах по 10 кусочков нитрита йода
(йодида аммония). Два преподавателя, поднимаясь каждый по своей
лестнице на семинар по химии, наступают или нет на любой из этих кусочков
с вероятностью 1/2. Двух взрывов, как расчитывают студенты, достаточно,
чтобы неудачливый преподаватель решил не ходить на семинар.
а) С какой вероятностью в этот день в университете состоятся не все
занятия?
б) С какой вероятностью и Вася, и Коля, и оба преподавателя
в этот день пропустят занятия?
- 4.
- В первой папке 11 чистых бланков и 4 заполненных,
а во второй — 5 чистых и 7 заполненных.
Вася достает из наудачу выбранной папки 3 первых попавшихся бланка.
Найти вероятность того что:
а) все три бланка чистые;
б) ровно два из трех бланков чистые;
в) Вася выбрал первую папку, если все 3 бланка оказались чистыми.
- 5.
- Событие
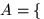 хотя бы одна из 10 стоящих на полке книг —
без картинок}, событие
хотя бы одна из 10 стоящих на полке книг —
без картинок}, событие 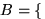 все 10 книг с картинками}. Что означает событие
а)
все 10 книг с картинками}. Что означает событие
а) 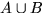 ; б)
; б) 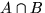 ;
в)
;
в) 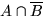 ; г)
; г) 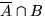 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 7 белых и 8 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [2, 4] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 5.
- 3.
- Студенты Вася Иванов и Коля Петров
(незнакомые друг с другом) готовят для своих друзей по
праздничному ужину каждый. Вася и Коля собирают грибы.
В роще, где ходит Вася, всего 8 грибов, и каждый
из них с вероятностью 1/2 оказывается мухомором. То же самое
относится к сосновому лесу, где собирает грибы Коля. По рецепту
требуется не менее двух мухоморов, чтобы приготовить праздничный ужин.
а) С какой вероятностью состоится хотя бы один праздничный ужин?
б) С какой вероятностью и Вася, и Коля смогут приготовить любимое
блюдо?
- 4.
- В левой миске — 12 кусочков «Chappi» и 3 кусочка
«Pedigree», а в правой — 5 «Chappi» и 8 «Pedigree».
Сытый пес Тобик выбирает наудачу миску и съедает из нее 3 кусочка.
Найти вероятность того что:
а) все три съеденных кусочка — «Chappi»;
б) ровно два из трех кусочков — «Chappi»;
в) Тобик выбрал левую миску, если все 3 съеденных кусочка
оказались «Chappi».
- 5.
- Событие
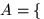 все 5 задач решены правильно}, событие
все 5 задач решены правильно}, событие 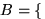 хотя бы одна из 5 задач решена неправильно}. Что означает событие
а)
хотя бы одна из 5 задач решена неправильно}. Что означает событие
а) 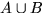 ; б)
; б) 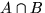 ;
в)
;
в) 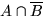 ; г)
; г) 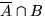 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 6 белых и 9 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [0, 2] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 6.
- 3.
- Студенты Вася Иванов и Коля Петров в столовой
выбирают из 7 ножичков для чистки яблок
и 7 вилочек для рыбы два ножа и две вилочки.
Любой нож или вилочка для рыбы с вероятностью 1/2 оказываются
погнутыми, что друзьям совсем не нравится.
Они заранее готовы даже ограничиться либо только двумя ножичками
для чистки яблок, либо только двумя вилочками для рыбы.
а) С какой вероятностью друзьям удастся пообедать?
б) С какой вероятностью они найдут все
необходимые столовые предметы?
- 4.
- В левой папке 11 открыток «С Новым Годом» и
4 — «С днем рождения»,
а в правой — 5 «С Новым Годом» и 8 «С днем рождения».
Вася достает из наудачу выбранной папки 3 первые попавшиеся открытки.
Найти вероятность того что:
а) все три открытки — «С днем рождения»;
б) ровно две из трех открыток — «С днем рождения»;
в) Вася выбрал левую папку, если все 3 открытки оказались
«С днем рождения».
- 5.
- Событие
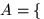 хотя бы одна из 8 встреченных собак —
не бульдог}, событие
хотя бы одна из 8 встреченных собак —
не бульдог}, событие 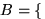 все 8 встреченных собак — бульдоги}. Что означает событие
а)
все 8 встреченных собак — бульдоги}. Что означает событие
а) 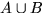 ; б)
; б) 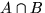 ;
в)
;
в) 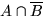 ; г)
; г) 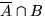 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 5 белых и 10 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [1, 3] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 7.
- 3.
- Чтобы заработать, студенты Вася Иванов и
Коля Петров решают друг для друга задание по теории вероятностей.
Каждая из 9 имеющихся у Васи и каждая из 9 имеющихся у Коли
задач оказывается решена правильно с вероятностью 1/2
независимо от остальных. Чтобы получить положительную оценку,
нужно решить правильно не менее двух задач из предложенных 9.
а) С какой вероятностью хотя бы одному из студентов повезет?
б) С какой вероятностью оба студента получат положительные оценки?
- 4.
- В левой миске — 11 кусочков «Whiskas» и 4 кусочка
«KiteKat», а в правой — 5 «Whiskas» и 9 «KiteKat».
Сытый и ленивый кот Борис выбирает наудачу миску и съедает
из нее 3 кусочка. Найти вероятность того что:
а) все три съеденных кусочка — «Whiskas»;
б) ровно два из трех кусочков — «Whiskas»;
в) Борис выбрал левую миску, если все 3 съеденных кусочка
оказались «Whiskas».
- 5.
- Событие
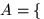 все 7 вынутых из урны шариков черные}, событие
все 7 вынутых из урны шариков черные}, событие 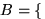 хотя бы один из 7 вынутых шариков не черный}. Что означает событие
а)
хотя бы один из 7 вынутых шариков не черный}. Что означает событие
а) 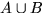 ; б)
; б) 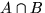 ;
в)
;
в) 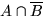 ; г)
; г) 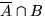 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 4 белых и 11 черных шаров. Вася и Петя по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [2, 4] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 8.
- 3.
- 5 студентов и 5 студенток ЭФ бегут на лыжах, соответственно,
пятерку и тройку. Любой(ая) из 10 лыжников с вероятностью
1/2 решается сократить свой маршрут на четверть.
На выходе на тройку хитрых лыжниц ожидает И.Б.Ткаченко,
а на пятерке с той же целью спрятался В.Н.Серов.
Каждый из них останется доволен результатами бега,
если поймает не менее двух хитрых студентов (студенток).
С какой вероятностью
а) хотя бы один из тренеров б) они оба
останутся довольны результатами бега?
- 4.
- В первом аквариуме — 9 барбусов и 6
пицелий, а во втором — 4 барбуса и 7 пицелий.
Кот Борис наудачу выбрал аквариум и поймал в нем 3 рыбки.
Найти вероятность того что:
а) Борису попались три барбуса;
б) ровно две из трех пойманных рыбок — барбусы;
в) Борис выбрал первый аквариум, если все 3 съеденных рыбки
оказались барбусами.
- 5.
- Событие
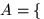 хотя бы один из 12 студентов
знает ЗБЧ}, событие
хотя бы один из 12 студентов
знает ЗБЧ}, событие 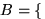 все 12 студентов не знают ЗБЧ}. Что означает событие
а)
все 12 студентов не знают ЗБЧ}. Что означает событие
а) 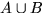 ; б)
; б) 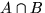 ;
в)
;
в) 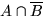 ; г)
; г) 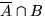 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 3 белых и 12 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [0, 2] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 9.
- 3.
- В двух ящиках сложены б/у модули памяти SIMM - по 11 штук в каждом.
Каждый модуль памяти с вероятностью 1/2 оказывается негодным.
Студенты Вася Иванов и Коля Петров ищут, каждый в своем ящике,
модули памяти для сборки (каждый своего) компьютера. Предполагая,
что на каждый компьютер нужно два модуля памяти,
и друзья ни за что не поделятся друг с другом
найденными модулями памяти, найти, с какой вероятностью
а) хоть один из компьютеров заработает;
б) удастся собрать оба компьютера.
- 4.
- В первой стопке 10 книг по экономике и
5 по мат. анализу,
а во второй — 4 по экономике и 7 по мат. анализу .
Вася достает из наудачу выбранной стопки 3 первые попавшиеся книги.
Найти вероятность того что:
а) все три книги — по экономике;
б) ровно две из трех книг — по экономике;
в) Вася выбрал левую стопку, если все 3 книги оказались
по экономике.
- 5.
- Событие
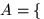 хотя бы один из 6 телевизоров не работает}, событие
хотя бы один из 6 телевизоров не работает}, событие 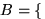 все 6 телевизоров исправны}. Что означает событие
а)
все 6 телевизоров исправны}. Что означает событие
а) 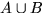 ; б)
; б) 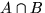 ;
в)
;
в) 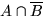 ; г)
; г) 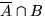 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 2 белых и 13 черных шаров. Вася и Петя по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [2, 4] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 2.
- 3.
- На доске объявлений ЭФ висят два листка для записи
на спецкурсы. У каждого листка в полном недоумении стоят по 4 студента.
Первые четверо думают, с одной «м» или с двумя пишется слово
«имитация». Еще четверо гадают, не добавить ли букву «ф»
в слово «офис». В итоге каждый принимает решение наудачу
и независимо от остальных («правильно» или «нет» с вероятностью 1/2).
На листке делаются исправления, если хотя
бы двое из 4 стоящих около него студентов решили,
что слово написано неверно.
а) С какой вероятностью хоть одно из слов окажется «исправленным»?
б) С какой вероятностью студенты «исправят» оба слова?
- 4.
- Перед Колей — 2 колоды карт. В левой колоде 10 красных
и 3 черных, а в правой — 3 красных и 9 черных.
Коля закрывает глаза и из наудачу выбранной колоды карт
достает 3 карты. Найти вероятность того что:
а) все три карты красные;
б) ровно две из трех карт красные;
в) Коля выбрал левую колоду, если все 3 карты оказались красными.
- 5.
- Событие
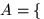 хотя бы одна из 4 страниц содержит
опечатки}, событие
хотя бы одна из 4 страниц содержит
опечатки}, событие 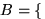 все 4 страницы без опечаток}. Что означает событие
а)
все 4 страницы без опечаток}. Что означает событие
а) 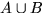 ; б)
; б) 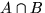 ;
в)
;
в) 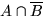 ; г)
; г) 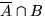 ?
?
При каких условиях события A и B окажутся независимыми?
- 1.
- В урне 1 белый и 14 черных шаров. Вася и Коля по
очереди достают по одному шарику. Если шарик черный, он возвращается
обратно. Выигрывает тот, кто первым вынет белый шар. Найти вероятность
выигрыша Васи.
- 2.
- На отрезок [0, 2] наудачу бросается точка. Найти вероятность
того, что у полученного числа (координаты этой точки) вторая цифра после
запятой равна 3.
- 3.
- Живущие в разных комнатах (в противоположных концах)
общежития Вася Иванов и Коля Петров проводят эксперимент,
бросая, каждый из своего окна,
пакеты с водой на проходящих под окном друзей. Всего у Васи и Коли
по 7 пакетов с водой. Каждый вовлеченный в эксперимент с равной
вероятностью возвращается либо к себе в комнату, либо в комнату
к экспериментатору. Для того, чтобы открыть крепкую дверь в комнату,
нужны по крайней мере двое очень рассерженных друзей.
а) С какой вероятностью в общежитии станет меньше целых дверей?
б) С какой вероятностью целых дверей станет меньше на две?
- 4.
- В первом ящике — 9 старых и 4 новых теннисных мяча,
а во втором — 3 старых и 9 новых.
Вася достает 3 мяча из наудачу выбранного ящика.
Найти вероятность того что:
а) все три мяча новые;
б) ровно два из трех мячей новые;
в) Вася выбрал первый ящик, если все 3 мяча оказались новыми.
- 5.
- Событие
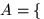 все 9 лампочек в люстре горят}, событие
все 9 лампочек в люстре горят}, событие 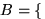 хотя бы одна из 9 лампочек не горит}. Что означает событие
а)
хотя бы одна из 9 лампочек не горит}. Что означает событие
а) 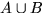 ; б)
; б) 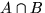 ;
в)
;
в) 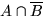 ; г)
; г) 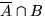 ?
?
При каких условиях события A и B окажутся независимыми?