(c) N.Chernova

Все фразы, формулы и термины выбраны из контрольных, тестовых и экзаменационных работ
по теории вероятностей и математической статистике
ЭФ, 1 курс, 1998 г., ММФ, 3 курс, 1998 г., ЭФ, 2 курс, 1998 г. и ММФ, 3 курс, 2002 г.

Как правило, формулировки задач пишутся так, наши комментарии — так, ответы студентов — так.

Теория вероятностей с иллюстрациями и комментариями
в изложении 1-го курса ЭФ

Cобытия бывают разные. Кроме «достоверного» и «невозможного», встречается редкий подвид — «случайное» событие. Некоторые исследователи считают, что этот подвид возник в результате скрещивания вида «событие» с видом «случайная величина» и является генетически неустойчивым. Мы склонны с ними согласиться. Под микроскопом можно увидеть самых мелких представителей вида «событие», известных под названием «элементарные исходы». Разница между достоверным событием и событием, которое случается со 100%-й вероятностью, невооруженному глазу недоступна. Именно поэтому неопытный энтомолог и склонен событие 100%-й вероятности трактовать как происходящее «всегда». Точно так же невооруженный глаз не отличит, за мелкостью, события нулевой вероятности от события невозможного или же «никогда не бываемого».

Hу а «у нас так глаз пристрелямши», и мы-то уж с вами легко согласимся, что нулевую вероятность умеют иметь не только пустые множества. После чего останется только признать, что можно иметь единичную вероятность и не быть при этом достоверным событием.

Вот и задача на пройденную тему и варианты ее "решения".

Задача: Привести пример события А, вероятность которого равна 1, но которое не является достоверным событием Ответы на письменном экзамене:
	После осени зима
	Похоже, что-то не так в этой вселенной. На всякий случай, исключать возможность катаклизмов и мы не будем.
	Можно предложить параметр времени. Например: что-то выйдет из строя (обязательно Р(А)=1) — но не в точный момент времени. Например: не в данную минуту
	Автор имел в виду абсолютно непрерывное распределение. И намекал на вероятность (не) попасть в точку (примечание переводчика).
	Из двух подбрасываний правильной монеты хотя бы раз выпадет решка: Р(А)=1/2+1/2=1
	У нас еще правильнее монета есть: из десяти подбрасываний нашей правильной монеты хотя бы раз выпадет решка с вероятностью Р(А)=1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2=5. Это-то уж точно достоверное событие.
	Монета, у которой с двух сторон один и тот же рисунок
	Вы уже поняли, какое событие имел в виду автор?
	Р(А)=P(xО[-1, 1])=1, но если x — длина стороны квадрата, то A не достоверно
Задача: Привести пример события A, вероятность которого равна 0, но которое не является невозможным событием Ответы на том же экзамене, но в другом варианте:
	Я получу оценку «4»
	Жаль, вопрос не на «4». А какой был бы парадокс! Не хуже, чем с брадобреем (который должен был брить тех, и только тех, кто не бреется сам).
	На Марсе живут земляне
	Эк все нас то в космогонию, то в космозоологию тянет. Хотя кто их, этих вездесущих землян, знает — вдруг и впрямь живут? Хотя бы с нулевой вероятностью, а?
	Событие, которое возможно, но при наступлении каких-то других его вероятность равна 0
	А это — типичный образец «ценных указаний», когда отвечать надо, но очень не хочется.

Что можно делать с вероятностями? Вы думаете, умножать, делить и складывать? Ошибаетесь. Их лучше пересекать и объединять. В отличие от событий, которые как раз при перемножении и делении начинают сверкать новыми гранями. Итак, новая алгебра множеств.

Задача:  Если события A1 и A2 несовместны, то они зависимы если (и только если) . . . ? (Продолжить)
	Ответ: . . . вероятность их пересечения равна пересечению их вероятностей
Задача:  Чему равна вероятность объединения n событий?
	Ответ: Объединению вероятностей событий
Задача:  Вероятность достоверного события равна . . . ?
	Ответ: A / W
Задача:  Как вычисляется Р(А) в классической вероятностной схеме?
	Ответ: Р(А)=A / n,   n — число экспериментов

С классиками и вовсе беда. Нерадивые какие-то у нас классики. То одно забудут, то другое.

	Чебышев не указывал, что величины должны быть с конечным 1-м моментом, а в условие входит конечность дисперсии
	Явно смухлевал Пафнутий Львович! И как же это он закон больших чисел доказал, если одна только дисперсия конечна?! А вот тут мы его и спросим: а мат. ожидание как же-с?

Каких только не бывает случайных величин! И таких не бывает, и эдаких не бывает. Самая популярная в НГУ (по многолетним наблюдениям) «случайная величина» — равномерно распределенная на всей прямой. Эта популярность очень избирательна: на ММФ, ЭФ и ФЕН такую величину любят студенты, на ФФ — преподаватели :-)). Ухожу, ухожу...

Вот зато какие они бывают (мифы, легенды, предания):

	Несовместные с. в. x и h
	Знакомьтесь: студент и явно несовместные с ним случайные величины x и h.
	Нормальное распределение на отрезке [0, 2]
	Остается добавить — «с вероятностью успеха 1/2 и интенсивностью l».
Задача:  Опишите класс с. в., для которых Ex2000=0
	Ответ: Это функции, у которых плотность — функция нечетная
В той же работе другая задача: может ли плотность распределения быть нечетной функцией? И ответ: «Да».
	Как минимум, последовательно и внутренне непротиворечиво. А с точки зрения математического анализа и весьма разумно: для нечетных «плотностей»  f  (жаль, что не только для них) Другое дело — бывают ли нечетные плотности?  Или пойти поискать?...
Еще ответ на ту же задачу:
	Если рассматривать Ex как центр тяжести, то x должна быть равномерно распределена по всей числовой прямой
	Вот наконец и оно, любимое, — равномерное на всей прямой, — и к любому случаю подходящее. Как оно там: A и "не A" вместе влечет все, что угодно? Или так: пустое множество есть подмножество любого другого? Нет, лучше вот так:   ∀ψ (¬φ → (φ → ψ)) .   Коротко и ясно.

Мы-то с вами понимаем глубокий философский смысл, вложенный авторами в ответы. Но разве эти испорченные преподаватели в состоянии оценить искрометную выдумку? Почувствовать всю прелесть результата предельного перехода? Увидеть, какие глубины мироздания открываются, лишь стоит допустить возможность исчезновения массы в никуда и появления оной из ничего? Серые они, право слово.

Чем отличается командная строка от GUI? Примерно тем же самым, чем HTML-редактор Emax (Edit, NotePad, etc., кому уже стало плохо — F4 :) отличается от FrontPage. А именно — вот чем.

Представьте себе, Вам крайне необходима случайная величина с экспоненциальным распределением. А датчик случайных чисел генерирует исключительно равномерно распределенные случайные числа. Вот мы Вас и поймали — Вам нужно знать квантильные преобразования!

«Ничего подобного», — отвечаете вы. - «Беру Excel (MathLab, Statistics, Maple etc.) — он все сам сделает. Я и знать не буду, как».

Так какое, говорите, место занял НГУ на последней (а также предпоследней) олимпиаде по программированию?

А вот и задача:  Случайная величина x имеет непрерывную и монотонную функцию распределения F(x).   Как распределена с. в. h=F(x ) ?

Ответ(ы):

Непрерывно и монотонно.   Варианты:  монотонно; имеет распределение N(a,s2)

И еще много-много красивых терминов (экономисты) и формул (математики), никакого отношения не имеющих к этому самому популярному в экономическом, статистическом и математическом моделировании преобразованию распределений случайных величин (aka квантильному преобразованию).

Как много в теории вероятностей терминов и обозначений! Многие из них имеют вполне привычный вид, означая при этом что-то новое, непонятное и страшное!

— Что это за стрелочка: ""?

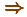— Стремится!

— Куда?

— Туда! — И рукой эдак слева направо...

(Экзамен по Т.В. на ММФ НГУ, 1998 г.)

Задача:  Оценить вероятность отклонения с. в. x от своего среднего значения на величину большую, чем 4 корня из дисперсии.

Вот эти "четыре корня из дисперсии" в одной работе:

.

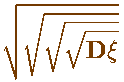Попробуйте-ка сказать, что это не «4 корня из дисперсии»!

А это тоже они — в другой работе:

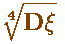
Или, скажем, задача начинается так:  Пусть 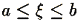п. н.

Комментарий студента на полях:

p =1,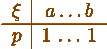

П. н. означает "почти наверное", или "с вероятностью 1". Как все-таки по-разному люди понимают простую надпись: "С вероятностью 1 значения случайной величины x лежат между a и b"!    Каламбур-с...

Как вы думаете: если 143 студента 1 курса ЭФ одновременно рисуют график одной и той же функции, сколько существенно различных графиков получится? Если вы ответили "143" — вы угадали! Если меньше — вы невнимательно читали эту страницу с самого начала или сильно недооцениваете фантазию экономистов.

Из экономии места, времени и информационных ресурсов человечества мы выбрали из 143*3 графиков самые красивые. 143*3 — это по 143 к каждой из трех задач :-).

Функции распределения случайной величины с одним и тем же распределением Пуассона с одним и тем же параметром l.

Функции распределения случайной величины    x = const  п. н. На этот раз константы разные — сначала "5", через две недели — меньше: "0" или "1".

И третья задача:  Производится один опыт, в результате которого может произойти событие A (с вероятностью 0.2).
Рассматривается случайная величина x,  равная 1, если A произошло, и 0, если A не произошло.
Нарисовать функцию распределения x.

Функции распределения случайной величины с распределением Бернулли (вариант от варианта слабо отличался вероятностью успеха — 0.2 или 0.7. Имеется в виду успех в испытании схемы Бернулли).

Вы видели графики? Нет, вы не видели графиков! Какая точка на вещественной оси: "А произошло"! Только положительная почему-то...

Как вы думаете, как выглядит график функции 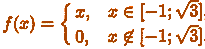  ? Можно побиться об заклад, что вы ошибаетесь. Потому что выглядит он так:

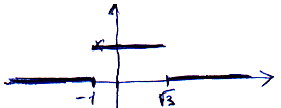
А вот и финал. Печальный уже своей неизбежностью. Но очень радующий уникальностью (то есть неповторяемостью).

Вопрос:  Ограничена ли вероятность события?

Ответ:  Нет

Продукт математического образования
ММФ, 3 курс, письменный экзамен по математической статистике

Эту главу можно смело читать даже тем, кто не имеет ни малейшего понятия о математической статистике. Мы не будем касаться вещей специальных. Ведь уже к моменту начала изучения математической статистики студент ММФ с ужасом обнаруживает, что от него требуется (страшное дело!) уметь дифференцировать, интегрировать и решать неравенства с модулями. А еще нужно знать, что такое предел последовательности — мыслимо ли это?! Нет, все-таки страшная вещь — статистика!

Студенты ММФ обычно немногословны. Поэтому ниже представлены в основном формулы, снабженные нашими комментариями. Но какие формулы!

	Нестандартный анализ:
	Откуда такое берется? Вот отсюда, например:
	Можно еще и так, но это уже не для всех: если c =3,  то   Под интегралом, как водится, плотность постоянной c.

	А вот и условная вероятность:
	Решаем неравенство с модулем:

Неравенства такого типа (чтоб вы знали) решаются просто: берем 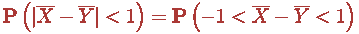   и переворачиваем знаки неравенств в обратную сторону. Все!

И еще раз решаем. Заметьте — последняя вероятность все-таки равна нулю: тут еще не все потеряно!

А вот критерий. Да еще и наиболее мощный:

Критерий — это всего только способ выбора одной из двух (в данном случае) гипотез ( H₁ или H₂ ) в зависимости от выборки. Как вы думаете, какая из гипотез больше нравится автору ответа? И чему все-таки равна эта "наибольшая", как утверждается, мощность данного критерия, то есть вероятность при верной гипотезе H₂ ее же и выбрать? И не маловато ли будет? И, наконец, при чем тут выборка?

Читая классиков:

Распределение Бирнуля

О, Бирнуль! Результат фонетического анализа, проведенного одним из студентов ЭФ, проливает свет на это имя: бир — один (казах.), нуль — ноль (русск.).

Теорема Фшире.   Вариант:   теорема Шифера.

Пример Кантора — Валесница.

(Из тетради с лекциями, ММФ, 2002). На вопрос «кто такой Валесниц?» автор предположил, что это какой-то польский математик.

ЗБЧ в форме Кинчева  (ММФ, 2002).

Слова, слова, слова...

. . . так как стоит единица, которая очень сильно мешает...

. . . можем пронести по теореме Лебега

Нормальное распределение:   N(a1-a2, 0)

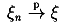Вопрос: Вытекает ли из сходимости по вероятности  сходимость ?

Ответ: 

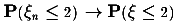Да. xn сходится к x по вероятности, следовательно, слабо сходится. Одно из определений слабой сходимости — сходимость функций распределения в точках непрерывности. 2 — точка непрерывности, поэтому . . .

Вопрос армянскому радио:
— Может ли в точке x=2 функция иметь разрыв?
— Ну что вы! Это же такая хорошая точка!

Худсон Д., "Статистика для физиков", Мир, 1970:

Конечное и бесконечное в математике:    (при  , очевидно)

А вы говорите — "ЗБЧ, ЗБЧ" . . .  ЦПТ!

(опять же, при  )

Образец IF — THEN — ELSE конструкций:  если 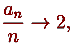  то , иначе — еще хуже.

Уже к началу знакомства с математической статистикой (т.е. сразу после курса теории вероятностей) среднестатистический студент бывает настолько убежден в великом могуществе центральной предельной теоремы (см. выше) и в нормальности распределения всего сущего (еще выше), что разубедить его в этом не под силу никакому здравому смыслу.

Диалог при сдаче расчетного задания над выборкой из равномерного распределения на отрезке [0, q] :

— Имеет ли среднее арифметическое 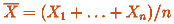   нормальное распределение?

— Да, конечно, с параметрами q / 2 и q ² / (12 n).

— Давайте возьмем n = 1. Имеет ли X ₁ нормальное распределение?

— Разумеется, с параметрами q / 2 и q ² / 12 .

— Да, но ведь X ₁ имеет равномерное распределение, как с этим быть?

— (пауза) А оно имеет одновременно и то, и другое распределение!

(Из воспоминаний одного преподавателя)

Это — что говорят. А вот что пишут:

Задача: Имеет ли среднее арифметическое n независимых случайных величин с равномерным распределением на отрезке 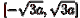 нормальное распределение? Если "да", то с какими параметрами?

Ответы не отличаются разнообразием: на N решений приходится N-3 "да". И параметры есть. Некоторые из этих "да" вы можете увидеть в подробностях:

Может, мы чего не понимаем, а?

А вот чем кончается изучение теории вероятностей на 1 курсе:
ЭФ, 2 курс, контрольные работы по математической статистике

Декабрь и май — время бесплодных надежд преподавателей и студентов. Первых — на то, что хотя бы в этом году обойдется без слишком отрицательных или уж очень положительных вероятностей, ну а вторых, как обычно, на то, что и такие сойдут.

— Да у Вас же вероятность отрицательна!?

— Я все правильно делал, давайте проверим выкладки!

(Из воспоминаний об ЭФ одного профессора)

Квантили: квартили, децили, процентили, а еще восьмили и десятили

Квантили уровня  –2,5 и   –8.

Не пугайтесь, это всего только точки, в которых функция распределения (вероятность чего-то там, кажется) равняется как раз     –2,5 или –8.

Вероятность ошибки 2-го рода стремится к –

Или

(опять же, при )

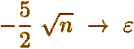
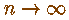Ксюгма и зюгма: о пользе языков изучения

. . . от ксюгмы.

От q ("theta", "тэта"), то есть. А говорят, еще вторая есть — "зюгма". И кто бы это?

ЗБЧ в форме Чернышева  (ЭФ, 2007).

В общем, понятно, кого с кем тут скрестили...

Вероятностная осень-98: хиты сезона

Посмотреть это нельзя. Это можно было только услышать.

Получается 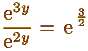, я только забыла — y сокращается или остается? (ЭФ, 774)

Извините, я не догадалась, чему равно 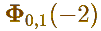 (того же автора)

Комментарий: речь идет о функции распределения гауссовского закона, существующей лишь в табличном виде

Посчитал математическое ожидание и дивергенцию случайной величины (ММФ, 602)

Распределение Стьюдента с n степенями защиты (ЭФ, 771)

Закон больших чисел Хинчена (ЭФ, 271)

Комментарий: это уже достижения не польских, а китайских математиков: Хин-Чен, Ли-Си-Цын

Зачет по теории вероятностей
ММФ, 3 курс, декабрь 2002 – январь 2003

Намеки авторов на авторство принимаются по е-mail cher@nsu.ru
Авторизуем. Навешиваем копирайт. Запросто.
Спешите прославить в веках свое имя! Страна хочет знать своих героев!