Все фразы, формулы и термины выбраны из контрольных и экзаменационных
работ
по теории вероятностей и математической статистике
ЭФ, 1 курс, 1998 г.,
ММФ, 3 курс, 1998 г. и
ЭФ, 2 курс, 1998 г.
Как правило, формулировки задач пишутся
так ,
наши комментарии - так ,
ответы студентов - так .

Теория вероятностей с иллюстрациями и комментариями
в изложении 1-го курса ЭФ
События, увы, бывают разные. Кое-кто думает,
что достоверное событие - это то, что всегда случается.
Так вот (страшная тайна): достоверно событие не тогда, когда всегда
случается, а когда кроме него больше и случиться-то нечему.
А посему классическая формула Якоба Бернулли -
"вероятность есть степень достоверности,
и отличается от нее как часть от целого" -
есть только классическая формула в рамках классической
вероятностной
схемы с конечным числом равновозможных элементарных исходов,
где, конечно же, достоверные события (и только они) имеют вероятность 1.
В остальных случаях давайте
договоримся: можно иметь единичную вероятность и не
быть достоверным событием (какой ужас!).
А вот задача на пройденную тему и ее "решения".
Указание:
подобрать случайные эксперименты к ответам,
не имеющим отношения к теории вероятностей.
|
Задача:
Привести пример события А,
вероятность которого равна 1,
но которое не является достоверным
событием
|
|
Ответы на письменном экзамене:
|

|
После осени зима
|
Недостоверно, разумеется. И как тонко подмечено!
Имеется ввиду, надо полагать, что после нашей осени
в Австралии, скажем, наступает совсем не зима, а как раз наоборот.

|
Можно предложить параметр времени. Например: что-то выйдет из строя
(обязательно Р(А)=1) - но не в точный момент времени. Например: не в
данную минуту
|
Речь идет, как можно догадаться, об абсолютно непрерывном распределении.
Скажем, об экспоненциальном. И что-то еще о вероятности не попасть в точку...

|
Из двух подбрасываний правильной монеты хотя
бы раз выпадет решка: P(A)=1/2+1/2=1
|
Крутая такая монета! А у нас еще лучше есть:
из десяти подбрасываний нашей правильной монеты хотя
бы раз выпадет решка с вероятностью
P(A)=1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2+1/2=5.
Это-то уж точно достоверное событие!

|
Монета, у которой с двух сторон один и тот же рисунок
|
Жаль, не написано - какой! Будем думать...

|
 , но если
x - длина стороны квадрата,
то А не достоверно , но если
x - длина стороны квадрата,
то А не достоверно
|
Конечно, конечно! А если взять квадрат побольше, то А даже станет
невозможно...

События, кроме того, бывают невозможные. Вы думаете,
что невозможные события, напротив, не
бывают? Бывают, бывают...
Вот и задача о них, не бывающих.
Указание:
выйти на улицу и спросить у десяти прохожих: возможно ли
попасть точкой в точку на отрезке?
Ответившим "нет" разъяснить разницу между событием невозможным и возможным
с нулевой вероятностью. Вызвать "Скорую Помощь".
|
Задача:
Привести пример события А,
вероятность которого равна 0,
но которое не является невозможным
событием
|
|
Ответы на том же экзамене, но в другом варианте:
|

|
Я получу оценку "4"
|
Жаль, вопрос не на "4". А какой был бы парадокс!
Не хуже, чем с брадобреем (который должен был брить
тех, и только тех, кто не бреется сам).

|
На Марсе живут земляне
|
Ну-ну! С вероятностью, отличной от нуля, занесенные космическими
аппаратами земные микроорганизмы уже могли в условиях Марса
эволюционировать до человека. Дарвин-с!

|
Событие, которое возможно, но при наступлении каких-то других
его вероятность равна 0
|
Ага. Несовместное с "какими-то другими" называется.

Что можно делать с вероятностями? Вы думаете, умножать, делить
и складывать? Ошибаетесь. Их лучше пересекать и объединять.
В отличие от событий, которые как раз при перемножении и делении
начинают сверкать новыми гранями. Итак, новая алгебра множеств.
|
Задача:
Если события A1 и A2
несовместны, то они зависимы если (и только если) . . . ? (Продолжить)
|

|
. . . вероятность их пересечения равна пересечению их вероятностей
|
|
Задача: Вероятность достоверного события равна . . . ?
|

|
A / W
|
|
Задача: Как вычисляется P(A) в классической
вероятностной схеме?
|

|
R(A) = A / n,
n - число экспериментов
|

С классиками и вовсе беда. Нерадивые какие-то у нас классики. То
одно забудут, то другое.

|
Чебышев не указывал, что величины должны быть
с конечным 1-м моментом, а в условие входит конечность дисперсии
|
Явно смухлевал Пафнутий Львович! И как же это он закон больших чисел
доказал, если одна только дисперсия конечна?! А вот тут мы его и спросим:
а мат. ожидание как же-с?

Каких только не бывает случайных величин! И таких не бывает, и эдаких
не бывает. Самая популярная в НГУ (по многолетним наблюдениям)
"случайная величина" - равномерно распределенная на всей
прямой. Эта популярность очень избирательна: на ММФ, ЭФ и ФЕН
такую величину любят студенты, на ФФ - преподаватели :-)).
Ухожу, ухожу...
Вот зато какие они бывают (мифы, легенды, предания):

|
Несовместные с. в. x и
h
|
Знакомьтесь: студент и явно несовместные с ним случайные величины
x и
h.

|
Нормальное распределение на отрезке [0,2]
|
Остается добавить - "с вероятностью успеха 1/2 и интенсивностью
l".
|
Задача: Опишите класс с. в., для которых
Ex
2000=0
|

|
Это функции, у которых плотность - функция нечетная
|
В той же работе другая задача: может ли
плотность распределения быть нечетной функцией? И ответ:
"Да". Как минимум,
последовательно и внутренне непротиворечиво. А с точки зрения математического
анализа и весьма разумно: для нечетных "плотностей" f
(жаль, что не только для них)
Другое дело - бывают ли нечетные плотности? Или пойти поискать?...
|
Еще ответ на ту же задачу:
|

|
Если рассматривать
Ex как центр
тяжести, то x должна быть
равномерно распределена по всей числовой прямой
|
Вот наконец и оно, любимое, - равномерное на всей прямой, - и к любому
случаю подходящее. Как оно там:
A и "не A" вместе влечет все, что угодно?
Или так:
пустое множество есть подмножество любого другого?
Нет, лучше вот
так: 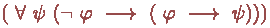 !
Коротко и ясно.
!
Коротко и ясно.

Чем отличается программирование на ассемблере
(паскале, C, etc.) от программирования на Delphi (etc.)?
Примерно тем же самым, чем HTML-редактор
MultiEdit (Edit, NotePad, etc., кому уже стало плохо - F4 :-)
отличается от FrontPage. А именно - вот чем.
Представьте себе,
Вам крайне необходима случайная величина
с экспоненциальным распределением. А датчик случайных
чисел генерирует исключительно равномерно распределенные случайные числа.
Вот мы Вас и поймали - Вам нужно знать квантильные преобразования!
"Ничего подобного", - отвечаете Вы. -
"Беру Excell (MathLab, Statistics, Maple etc.) - он
все сам сделает. Я и знать не буду, как."
Так какое,
говорите, место занял НГУ на последней олимпиаде по программированию?
|
А вот и задача: Случайная величина
x
имеет непрерывную и монотонную
функцию распределения F(x).
Как распределена с. в.
h = F ( x ) ?
|

|
Непрерывно и монотонно ( варианты: монотонно; имеет
распределение N(a,s2))
|
И еще много-много красивых терминов (экономисты) и формул (математики),
никакого отношения не имеющих к этому самому популярному в экономическом,
статистическом и математическом моделировании преобразованию распределений
случайных величин.

Как много в теории вероятностей терминов и
обозначений! Многие из них имеют вполне привычный вид,
означая при этом что-то новое, непонятное и страшное!
- Что это за стрелочка:
" 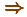 "?
"?
- Стремится!
- Куда?
- Туда!
- И рукой эдак слева направо...
(Экзамен по Т.В. на ММФ НГУ, 1998 г.)
|
Задача: Оценить вероятность отклонения с. в.
x
от своего среднего значения на величину большую, чем
4 корня из дисперсии.
|
|
Вот эти "четыре корня из дисперсии" в одной работе:
|

|
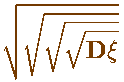 . .
|
Попробуйте-ка сказать, что это не "4 корня из дисперсии"!
|
А это тоже они - в другой работе:
|
|
Или, скажем, задача начинается так:
Пусть 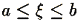 п. н. п. н.
|
|
Комментарий студента на полях:
|

|
p = 1, 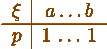
|
П. н. означает "почти наверное", или "с вероятностью 1".
Как все-таки по-разному люди понимают простую надпись:
"С вероятностью 1 значения случайной величины
x
лежат между a и b "! Каламбур-с...

Как Вы думаете: если 143 студента 1 курса ЭФ
одновременно рисуют график одной и той же функции,
сколько существенно различных графиков
получится? Если Вы ответили "143" - Вы угадали! Если меньше -
Вы невнимательно читали эту страницу с самого начала или
сильно недооцениваете фантазию экономистов.
Из экономии места, времени и информационных
ресурсов человечества мы выбрали из 143*3 графиков самые красивые.
143*3 - это по 143 к каждой из трех задач :-).

|
Функции распределения случайной величины с одним и тем же
распределением Пуассона с одним и тем же параметром
l.
|

|
Функции распределения случайной величины
x =
const п. н. На этот раз константы
разные - сначала "5", через две недели - меньше: "0" или "1".
Все равно не помогает!
|
|
И третья задача:
Производится один опыт, в результате которого может произойти событие A
(с вероятностью 0.2).
Рассматривается случайная величина
x, равная 1, если A
произошло, и 0, если A не произошло.
Нарисовать функцию распределения
x .
|

|
Функции распределения случайной величины
с распределением Бернулли (вариант от варианта слабо
отличался вероятностью успеха - 0.2 или 0.7. Имеется
ввиду успех в испытании схемы Бернулли).
|
Вы видели графики? Нет, Вы не видели графиков! Какая
точка на вещественной оси: "А произошло"!! Только положительная почему-то...
Как Вы думаете, как выглядит график
функции 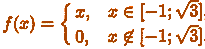 ?
Можно побиться об
заклад, что Вы ошибаетесь. Потому что выглядит он так:
?
Можно побиться об
заклад, что Вы ошибаетесь. Потому что выглядит он так:

А вот и финал. Печальный уже своей
неизбежностью. Но очень радующий уникальностью (то есть неповторяемостью).
|
Вопрос:
Ограничена ли вероятность события?
|

|
Нет
|

Продукт математического образования
ММФ, 3 курс, письменный экзамен по математической статистике
Эту главу можно смело читать даже тем, кто
не имеет ни малейшего понятия о математической статистике.
Мы не будем касаться вещей специальных. Ведь уже к моменту
начала
изучения математической статистики студент ММФ с ужасом обнаруживает,
что от него требуется (страшное дело!) уметь дифференцировать,
интегрировать и решать неравенства с модулями.
А еще нужно знать, что такое предел последовательности - мыслимо ли это?!
Нет, все-таки страшная вещь - статистика!
Студенты ММФ обычно немногословны. Поэтому ниже представлены в основном
формулы, снабженные нашими комментариями. Но какие формулы!

|
Нестандартный
анализ: 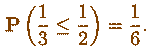
|

|
Откуда такое берется?
Вот отсюда, например: 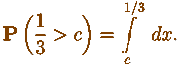
|

|
Можно еще и так, но это уже не для всех: 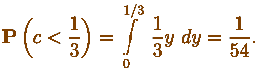 Под интегралом, как водится,
плотность постоянной c. Под интегралом, как водится,
плотность постоянной c.
|

|
А вот и условная вероятность:
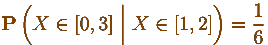
|

|
Решаем неравенство
с модулем: 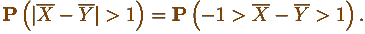
|
Неравенства такого типа (чтоб Вы знали) решаются просто: берем
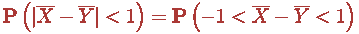 и переворачиваем знаки неравенств в обратную сторону. Все!
и переворачиваем знаки неравенств в обратную сторону. Все!

|
И еще раз решаем. Заметьте - последняя вероятность все-таки
равна нулю: тут еще не все потеряно!
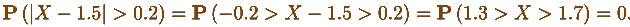
|

|
А вот критерий. Да еще и
наиболее мощный: 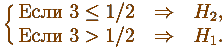
|
Критерий - это всего только способ выбора одной из двух (в данном случае)
гипотез ( H1 или H2 )
в зависимости от выборки. Как Вы думаете, какая из гипотез больше нравится
автору ответа? И чему все-таки равна эта "наибольшая", как утверждается,
мощность данного критерия, то есть вероятность при верной гипотезе
H2 ее же и выбрать? И не маловато ли будет?
Читая классиков:

|
Распределение Бирнуля
|
А в именительном падеже-то каково! Бирнуль!
Результат фонетического анализа, проведенного одним из студентов ЭФ,
проливает свет на это имя: бир - один (казах.),
нуль - ноль (русск.).

|
Теорема Фшире
|
Это которая "теорема Фишера". Как это получается у математиков,
даже экономисты комментировать не взялись.
Слова, слова, слова...

|
. . . так как стоит единица, которая очень сильно мешает...
|

|
. . . можем пронести по теореме Лебега
|

|
Нормальное такое распределение:
N(a1-a2, 0)
|
|
Вопрос:
Вытекает ли из сходимости по
вероятности 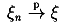 сходимость
сходимость 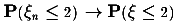 ? ?
|

|
Да. xn сходится к
x по вероятности, следовательно, слабо
сходится. Одно из определений слабой сходимости - сходимость функций
распределения в точках непрерывности. 2 - точка непрерывности,
поэтому... (и т.д.)
|
Вопрос армянскому радио:
- Может ли в точке x=2 функция иметь разрыв?
- Ну что вы! Это же такая хорошая точка!
Д. Худсон, "Статистика для физиков":

|
Конечное и бесконечное в математике:
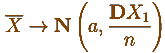 (при
(при 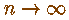 , очевидно) , очевидно)
|
А Вы говорите - "ЗБЧ, ЗБЧ" . . . ЦПТ!
Образец IF - THEN - ELSE конструкций:
если 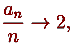 то
то  , иначе - еще хуже.
, иначе - еще хуже.

Уже к началу знакомства с математической
статистикой (т.е. сразу после курса теории вероятностей)
среднестатистический студент бывает настолько убежден
в великом могуществе центральной предельной теоремы (см. выше) и
в нормальности распределения всего сущего (еще выше),
что разубедить его в этом не под силу никакому здравому смыслу.
Диалог при сдаче расчетного задания над
выборкой из равномерного распределения
на отрезке [0 , q ] :
- Имеет ли среднее арифметическое
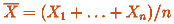 нормальное распределение?
нормальное распределение?
- Да, конечно, с параметрами
q / 2 и
q 2 /
(12 n).
- Давайте возьмем n = 1.
Имеет ли X1
нормальное распределение?
- Разумеется, с параметрами
q / 2 и
q 2 / 12 .
- Позвольте, да ведь
X1 имеет
равномерное распределение?
- (пауза) А оно имеет и то, и другое
распределение!
(Из недавних воспоминаний Д. А. Коршунова)
Это - что говорят. А вот что пишут:
|
Задача:
Имеет ли среднее арифметическое n независимых случайных величин с
равномерным распределением на
отрезке 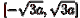 нормальное распределение? Если "да", то с какими параметрами?
нормальное распределение? Если "да", то с какими параметрами?
|
|
Ответы не отличаются разнообразием: на N решений приходится
N-3 "да". И параметры есть.
Некоторые из этих "да" Вы можете увидеть в подробностях:
|
Может, мы чего не понимаем, а?

И вот итог (как водится, печальный):

А вот чем кончается изучение теории вероятностей на 1 курсе:
ЭФ, 2 курс, контрольные работы по математической статистике
Ждем-с...

Намеки на авторство принимаются по е-mail
nat@cher.nsu.ru
Авторизуем. Навешиваем копирайт. Запросто.
Спешите! Страна хочет знать имена своих героев!



 , но если
x - длина стороны квадрата,
то А не достоверно
, но если
x - длина стороны квадрата,
то А не достоверно 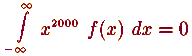
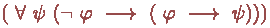 !
Коротко и ясно.
!
Коротко и ясно.
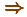 "?
"? 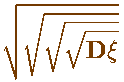 .
.
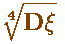
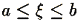 п. н.
п. н.
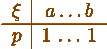
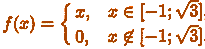 ?
Можно побиться об
заклад, что Вы ошибаетесь. Потому что выглядит он так:
?
Можно побиться об
заклад, что Вы ошибаетесь. Потому что выглядит он так:
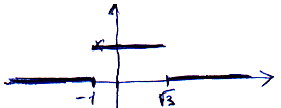
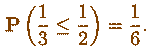
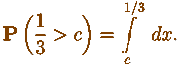
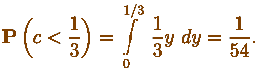 Под интегралом, как водится,
плотность постоянной c.
Под интегралом, как водится,
плотность постоянной c.
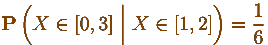
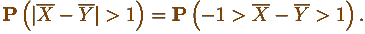
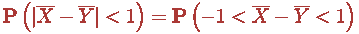 и переворачиваем знаки неравенств в обратную сторону. Все!
и переворачиваем знаки неравенств в обратную сторону. Все!
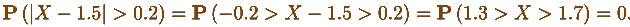
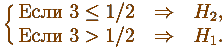
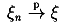 сходимость
сходимость 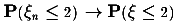 ?
?
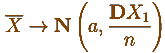 (при
(при 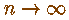 , очевидно)
, очевидно)
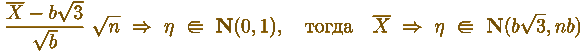 (опять же, при
(опять же, при 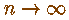 )
)
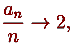 то
то  , иначе - еще хуже.
, иначе - еще хуже.
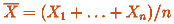 нормальное распределение?
нормальное распределение?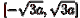 нормальное распределение? Если "да", то с какими параметрами?
нормальное распределение? Если "да", то с какими параметрами?