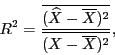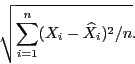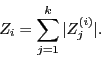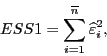Линейная регрессия
Рассмотрим вектор факторов регрессии
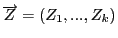 и вектор неизвестных параметров регрессии
и вектор неизвестных параметров регрессии
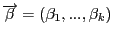 . Будем изучать линейную регрессию
. Будем изучать линейную регрессию
Пусть в 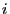 -м эксперименте факторы регрессии принимают заданные значения
-м эксперименте факторы регрессии принимают заданные значения
где 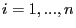 .
После
.
После 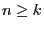 экспериментов получен набор откликов
экспериментов получен набор откликов 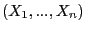 :
:
с матрицей плана 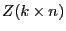
Матрицу 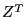 - будем называть матрицей линейного преобразования (собственно она и вводится в предлагаемом статистическом пакете),
вектор
- будем называть матрицей линейного преобразования (собственно она и вводится в предлагаемом статистическом пакете),
вектор
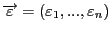 - будем называть вектором ошибок (случайных остатков).
Сформулируем следующую теорему.
- будем называть вектором ошибок (случайных остатков).
Сформулируем следующую теорему.
Теорема (Гаусс-Марков).
Пусть матрица 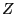 имеет ранг
имеет ранг 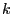 и вектор ошибок
и вектор ошибок
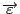 - состоит из независимых гауссовских случайных величин
с распределением
- состоит из независимых гауссовских случайных величин
с распределением
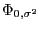 с одной и той же дисперсией. Тогда ОМНК
с одной и той же дисперсией. Тогда ОМНК
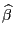 , которая минимизирует функцию
, которая минимизирует функцию
имеет вид:
Ковариационная матрица оценки
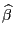 вычисляется по формуле:
вычисляется по формуле:
где
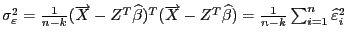 - несмещенная оценка для дисперсии случайного остатка (через
- несмещенная оценка для дисперсии случайного остатка (через
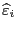 мы обозначили
мы обозначили 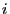 -ую компоненту вектора
-ую компоненту вектора
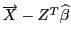 , компоненты этого вектора и являются оценками сл. остатков регрессии).
, компоненты этого вектора и являются оценками сл. остатков регрессии).
Обозначим
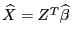 - "иксы" , вычисленные по линейному уравнению регрессии. Введем в рассмотрение характеристики регрессии, которые будут вычисляться в пакете. Прежде всего
отметим коэффициент детерминации
- "иксы" , вычисленные по линейному уравнению регрессии. Введем в рассмотрение характеристики регрессии, которые будут вычисляться в пакете. Прежде всего
отметим коэффициент детерминации
коэффициент детерминации показывает, какую долю выборочной дисперсии "иксов" составляет выборочная дисперсия "иксов", вычисленных
по уравнению регрессии, отметим, что чем ближе 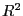 к единице, тем лучше регрессия аппроксимирует эмпирические данные. Далее среднеквадратической
погрешностью или ошибкой уравнения регрессии называется
к единице, тем лучше регрессия аппроксимирует эмпирические данные. Далее среднеквадратической
погрешностью или ошибкой уравнения регрессии называется
Особо отметим статистику Дарбина-Ватсона
На основе этой статистики строится критерий для проверки предпосылки теоремы Гаусса-Маркова о некоррелированности случайных остатков в модели
линейной регрессии, а именно, проверяется гипотеза
Сам критерий Дарбина-Ватсона здесь мы приводить не будем, скажем лишь то, что значения 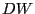 близкие к двойке говорят в пользу принятия гипотезы
близкие к двойке говорят в пользу принятия гипотезы 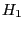 . Более подробно коснемся теста Голдфелда-Квандта. С помощью этого критерия проверяется предпосылка теоремы Гаусса-Маркова о совпадении дисперсий
случайных остатков в модели линейной регрессии (в эконометрике говорят проверяется гомоскедастичность сл. остатков).
В дальнейшем уравнения системы
. Более подробно коснемся теста Голдфелда-Квандта. С помощью этого критерия проверяется предпосылка теоремы Гаусса-Маркова о совпадении дисперсий
случайных остатков в модели линейной регрессии (в эконометрике говорят проверяется гомоскедастичность сл. остатков).
В дальнейшем уравнения системы
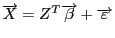 будем называть уравнениями наблюдений объекта. Итак, упорядочим уравнения наблюдений объекта по возрастанию суммы модулей
значений факторов регрессии, т.е. по возрастанию значений
будем называть уравнениями наблюдений объекта. Итак, упорядочим уравнения наблюдений объекта по возрастанию суммы модулей
значений факторов регрессии, т.е. по возрастанию значений
По первым 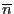 упорядоченным уравнениям (где
упорядоченным уравнениям (где 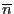 удовлетворяет условиям
удовлетворяет условиям
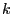 - количество оцениваемых параметров регрессии) вычисляем ОМНК
- количество оцениваемых параметров регрессии) вычисляем ОМНК
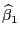 , затем находим
, затем находим
где, по-прежнему,
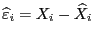 . Аналогично по последним
. Аналогично по последним 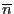 упорядоченным уравнениям наблюдений
вычисляем ОМНК
упорядоченным уравнениям наблюдений
вычисляем ОМНК
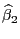 , затем также вычисляем
, затем также вычисляем 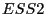 . В итоге получаем статистику, которую назовем статистикой
Голдфельда-Квандта
. В итоге получаем статистику, которую назовем статистикой
Голдфельда-Квандта
Реально достигнутый уровень значимости критерия вычисляется по формуле
где 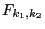 - функция распределения Фишера с
- функция распределения Фишера с
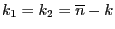 степенями свободы.
степенями свободы.
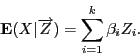
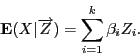
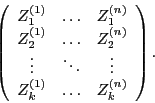
![]() - "иксы" , вычисленные по линейному уравнению регрессии. Введем в рассмотрение характеристики регрессии, которые будут вычисляться в пакете. Прежде всего
отметим коэффициент детерминации
- "иксы" , вычисленные по линейному уравнению регрессии. Введем в рассмотрение характеристики регрессии, которые будут вычисляться в пакете. Прежде всего
отметим коэффициент детерминации