Псевдослучайные числа.
Генерирование случайных чисел равномерно распределенных на отрезке 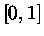 в данной работе происходит либо с помощью
встроенного в язык Java датчика случайных чисел (о котором автор имеет очень смутные представления), либо используется так называемый
линейный конгруэнтный метод (см. Д. Кнут "Искусство программирования для ЭВМ"), выбор того или иного генератора можно
сделать с помощью радиокнопок. Дадим краткое описание метода. Получим последовательность
в данной работе происходит либо с помощью
встроенного в язык Java датчика случайных чисел (о котором автор имеет очень смутные представления), либо используется так называемый
линейный конгруэнтный метод (см. Д. Кнут "Искусство программирования для ЭВМ"), выбор того или иного генератора можно
сделать с помощью радиокнопок. Дадим краткое описание метода. Получим последовательность 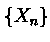 ,
следующим образом:
,
следующим образом: 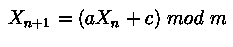 , где
, где 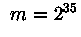 ,
,
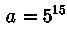 ,
, 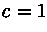 (выбор
(выбор 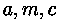 представляет собой весьма непростую задачу, смотрите по этому поводу упомянутую
монографию Д. Кнута).
Тогда последовательность
представляет собой весьма непростую задачу, смотрите по этому поводу упомянутую
монографию Д. Кнута).
Тогда последовательность 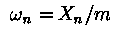 -
моделирует последовательность случайных чисел равномерно распределенных
на отрезке
-
моделирует последовательность случайных чисел равномерно распределенных
на отрезке 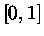 . Случайные величины, имеющие
непрерывную функцию распределения
. Случайные величины, имеющие
непрерывную функцию распределения 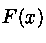 , можно генерировать, используя метод обратной
функции суть, которого состоит в том, что случайная величина
, можно генерировать, используя метод обратной
функции суть, которого состоит в том, что случайная величина 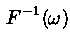 , где
, где
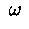 - сл. величина с
равномерным на
- сл. величина с
равномерным на 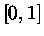 распределением,
имеет как раз распределение
распределением,
имеет как раз распределение 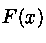 . Случайные величины, имеющие нижеследующие
плотности будут генерироваться именно методом обратной функции:
. Случайные величины, имеющие нижеследующие
плотности будут генерироваться именно методом обратной функции:
| Тип распределения и обозначение
| Плотность
|
|---|
Равномерное распределение, 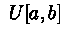
| 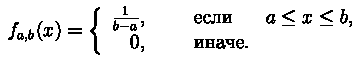
|
|---|
Экспоненциальное распределение, 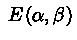
| 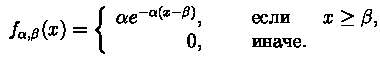
|
Распределение Коши, 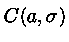
| 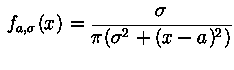
|
Распределение Вейбулла, 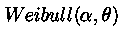
| 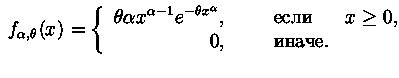
|
Распределение Парето, 
| 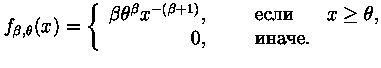
|
Распределение Лапласа, 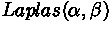
| 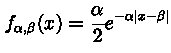
|
Рэлеевское распределение, 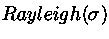
| 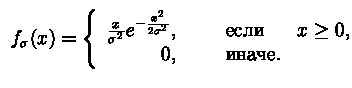
|
Гамма-распределение, 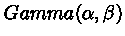
| 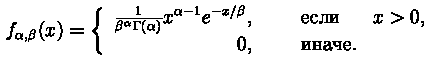
|
Распределение график плотности, которого имеет вид треугольника
со стороной на оси абсцисс, 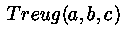 , ,
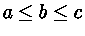 , , 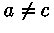
| 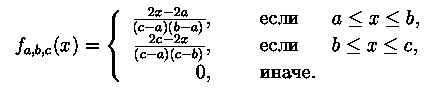
|
Определение всех плотностей распределений сл. величин, генерируемых в данной работе можно посмотреть
здесь.
В последнем случае, для примера, приведем вид 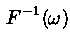 :
:
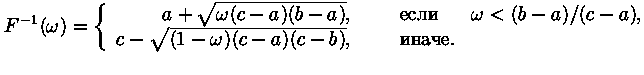
Стандартное нормальное распределение генерируется в данной работе методом полярных координат, а именно:
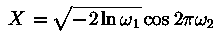 , где
, где 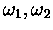 - независимые
равномерно распределенные на отрезке
- независимые
равномерно распределенные на отрезке 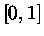 сл. величины, в этом случае (как легко проверить) сл. величина
сл. величины, в этом случае (как легко проверить) сл. величина
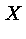 имеет стандартное нормальное распределение, далее можно получить нормальное
распределение
имеет стандартное нормальное распределение, далее можно получить нормальное
распределение 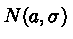 благодаря представлению
благодаря представлению
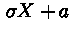 . Стандартное распределение Стъюдента генерируется исходя из представления:
. Стандартное распределение Стъюдента генерируется исходя из представления:
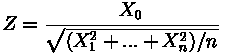 , где
, где 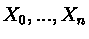 - независимые стандартные
нормальные сл. величины. Распределение Стъюдента
- независимые стандартные
нормальные сл. величины. Распределение Стъюдента  получается благодаря представлению
получается благодаря представлению
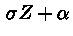 (плотность этого распределения можно увидеть
здесь.).
Теперь рассмотрим некоторые дискретные распределения.
(плотность этого распределения можно увидеть
здесь.).
Теперь рассмотрим некоторые дискретные распределения.
Распределение Бернулли, обозначение 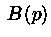 . Генерируется, используя равномерно
распределенные сл. величины. Положим
. Генерируется, используя равномерно
распределенные сл. величины. Положим 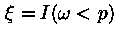 , где
, где
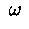 - сл. величина равномерно распределенная
на отрезке
- сл. величина равномерно распределенная
на отрезке 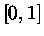 , а
, а
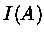 - индикатор множества
- индикатор множества 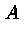 . В этом случае сл. величина
. В этом случае сл. величина
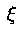 имеет бернулевское распределение.
имеет бернулевское распределение.
Биномиальное распределение, обозначение 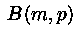 , вероятность
, вероятность
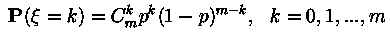 .
Известно, что сл. величину
.
Известно, что сл. величину 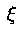 можно представить в виде суммы
можно представить в виде суммы
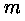 независимых одинаково распределенных бернулевских сл. величин, поэтому
становится очевидным то, как генерировать биномиальные сл. величины.
независимых одинаково распределенных бернулевских сл. величин, поэтому
становится очевидным то, как генерировать биномиальные сл. величины.
Пуассoновское распределение, обозначение 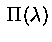 , вероятность
, вероятность
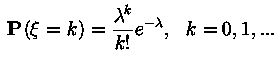 .
Генерируется исходя
из следующего равенства:
.
Генерируется исходя
из следующего равенства: 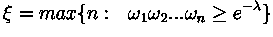 ,
,
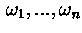 - независимые равномерно
распределенные на отрезке
- независимые равномерно
распределенные на отрезке 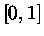 сл. величины.
сл. величины.
Геометрическое распредление, обозначение 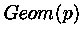 , вероятность
, вероятность
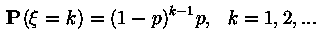 . Генерируется благодаря следующей удобной формуле:
. Генерируется благодаря следующей удобной формуле:
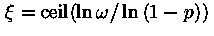 , где
, где 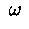 -
сл. величина равномерно распределенная на отрезке
-
сл. величина равномерно распределенная на отрезке
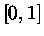 , а
, а
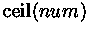 - операция округления числа
- операция округления числа
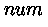 до ближайшего целого числа не меньшего, чем
до ближайшего целого числа не меньшего, чем
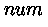 .
.
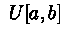
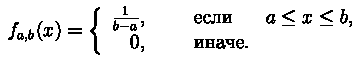
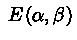
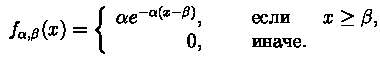
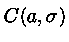
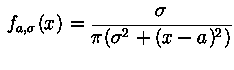
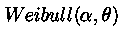
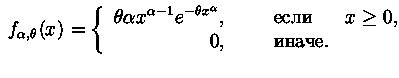

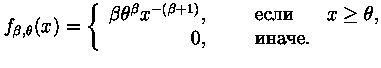
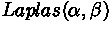
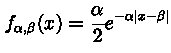
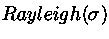
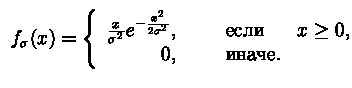
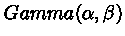
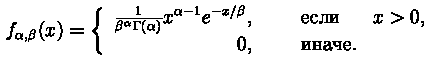
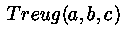 ,
,
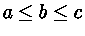 ,
, 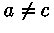
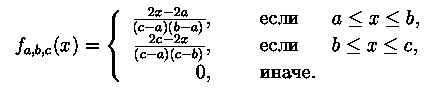
 в данной работе происходит либо с помощью
встроенного в язык Java датчика случайных чисел (о котором автор имеет очень смутные представления), либо используется так называемый
линейный конгруэнтный метод (см. Д. Кнут "Искусство программирования для ЭВМ"), выбор того или иного генератора можно
сделать с помощью радиокнопок. Дадим краткое описание метода. Получим последовательность
в данной работе происходит либо с помощью
встроенного в язык Java датчика случайных чисел (о котором автор имеет очень смутные представления), либо используется так называемый
линейный конгруэнтный метод (см. Д. Кнут "Искусство программирования для ЭВМ"), выбор того или иного генератора можно
сделать с помощью радиокнопок. Дадим краткое описание метода. Получим последовательность 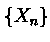 ,
следующим образом:
,
следующим образом: 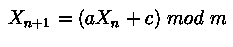 , где
, где 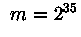 ,
,
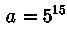 ,
, 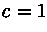 (выбор
(выбор 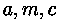 представляет собой весьма непростую задачу, смотрите по этому поводу упомянутую
монографию Д. Кнута).
Тогда последовательность
представляет собой весьма непростую задачу, смотрите по этому поводу упомянутую
монографию Д. Кнута).
Тогда последовательность 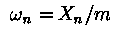 -
моделирует последовательность случайных чисел равномерно распределенных
на отрезке
-
моделирует последовательность случайных чисел равномерно распределенных
на отрезке 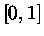 . Случайные величины, имеющие
непрерывную функцию распределения
. Случайные величины, имеющие
непрерывную функцию распределения 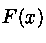 , можно генерировать, используя метод обратной
функции суть, которого состоит в том, что случайная величина
, можно генерировать, используя метод обратной
функции суть, которого состоит в том, что случайная величина 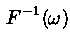 , где
, где
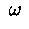 - сл. величина с
равномерным на
- сл. величина с
равномерным на 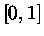 распределением,
имеет как раз распределение
распределением,
имеет как раз распределение 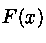 . Случайные величины, имеющие нижеследующие
плотности будут генерироваться именно методом обратной функции:
. Случайные величины, имеющие нижеследующие
плотности будут генерироваться именно методом обратной функции:
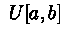
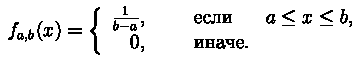
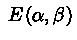
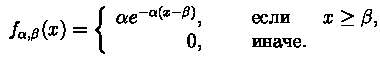
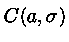
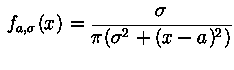
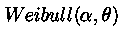
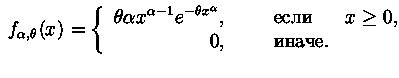

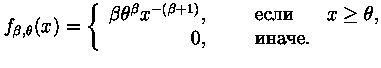
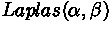
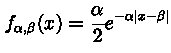
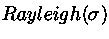
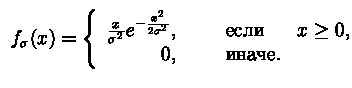
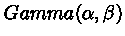
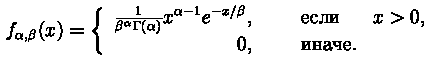
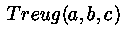 ,
,
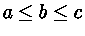 ,
, 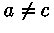
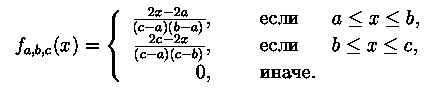
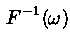 :
: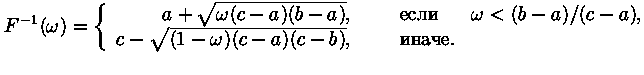
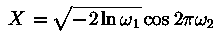 , где
, где 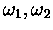 - независимые
равномерно распределенные на отрезке
- независимые
равномерно распределенные на отрезке 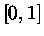 сл. величины, в этом случае (как легко проверить) сл. величина
сл. величины, в этом случае (как легко проверить) сл. величина
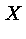 имеет стандартное нормальное распределение, далее можно получить нормальное
распределение
имеет стандартное нормальное распределение, далее можно получить нормальное
распределение 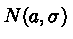 благодаря представлению
благодаря представлению
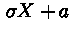 . Стандартное распределение Стъюдента генерируется исходя из представления:
. Стандартное распределение Стъюдента генерируется исходя из представления:
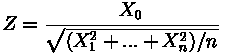 , где
, где 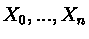 - независимые стандартные
нормальные сл. величины. Распределение Стъюдента
- независимые стандартные
нормальные сл. величины. Распределение Стъюдента  получается благодаря представлению
получается благодаря представлению
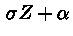 (плотность этого распределения можно увидеть
здесь.).
Теперь рассмотрим некоторые дискретные распределения.
(плотность этого распределения можно увидеть
здесь.).
Теперь рассмотрим некоторые дискретные распределения.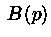 . Генерируется, используя равномерно
распределенные сл. величины. Положим
. Генерируется, используя равномерно
распределенные сл. величины. Положим 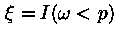 , где
, где
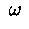 - сл. величина равномерно распределенная
на отрезке
- сл. величина равномерно распределенная
на отрезке 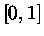 , а
, а
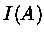 - индикатор множества
- индикатор множества 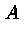 . В этом случае сл. величина
. В этом случае сл. величина
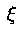 имеет бернулевское распределение.
имеет бернулевское распределение.
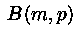 , вероятность
, вероятность
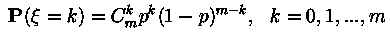 .
Известно, что сл. величину
.
Известно, что сл. величину 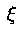 можно представить в виде суммы
можно представить в виде суммы
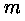 независимых одинаково распределенных бернулевских сл. величин, поэтому
становится очевидным то, как генерировать биномиальные сл. величины.
независимых одинаково распределенных бернулевских сл. величин, поэтому
становится очевидным то, как генерировать биномиальные сл. величины.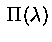 , вероятность
, вероятность
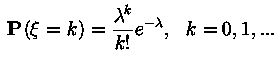 .
Генерируется исходя
из следующего равенства:
.
Генерируется исходя
из следующего равенства: 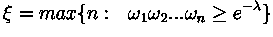 ,
,
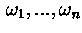 - независимые равномерно
распределенные на отрезке
- независимые равномерно
распределенные на отрезке 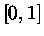 сл. величины.
сл. величины.
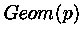 , вероятность
, вероятность
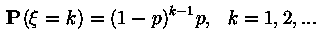 . Генерируется благодаря следующей удобной формуле:
. Генерируется благодаря следующей удобной формуле:
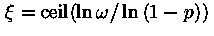 , где
, где 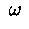 -
сл. величина равномерно распределенная на отрезке
-
сл. величина равномерно распределенная на отрезке
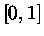 , а
, а
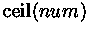 - операция округления числа
- операция округления числа
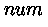 до ближайшего целого числа не меньшего, чем
до ближайшего целого числа не меньшего, чем
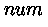 .
.