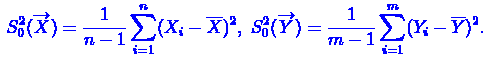
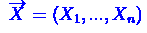из 
и
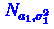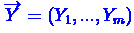из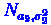 
.
Критерий Фишера проверяет гипотезу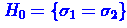 
.
Обозначим через 
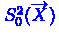и
несмещенные выборочные дисперсии:
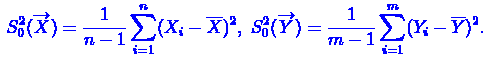
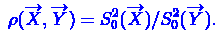
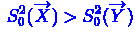. Пусть на
данных реализациях выборок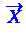 
и
получено число
.
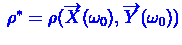Достигаемый уровень значимости в этом случае равен
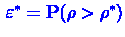. Тогда критерий Фишера
выглядит следующим образом: гипотеза 
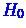принимается тогда и
только тогда, когда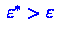 
.
Критерий Стъюдента. Пусть заданы две независимые выборки
из нормальных распределений 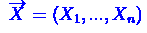из
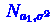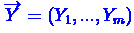и из
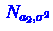с неизвестными средними и одной и той же
неизвестной дисперсией. Рассмотрим статистику Стъюдента:
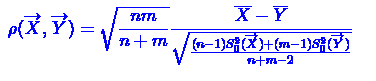
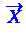и
получено число
.
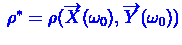Достигаемый уровень значимости в этом случае равен
.
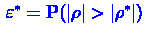Тогда критерий
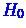Стъюдента выглядит следующим образом: гипотеза принимается
тогда и только тогда, когда .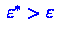
| Критерии согласия | |||
|---|---|---|---|
| Критерий Фишера | Критерий Стъюдента | ||
| Значение сатистики Фишера | Достигаемый уровень значимости | Значение статистики Стъюдента | Достигаемый уровень значимости |
| Реализация первой выборки |
|---|
| Реализация второй выборки |
|---|
С помощью радиокнопки выделяется проверяемый критерий, предлагается проверить либо критерий Фишера либо критерий Стъюдента.
Исследуемые выборки помещаются в текстовые поля (это можно сделать,
набрав соответствующие значения вручную либо скопировав, скажем из Excel), затем остается
нажать кнопку "Вычислить", после чего в текстовых полях "Значение статистики Фишера" и "Достигаемый уровень значимости"
либо "Значение статистики Стъюдента" и "Достигаемый уровень значимости" появится соответствующие значения.
Отметим, что в качестве десятичного разделителя в числах можно использовать и точку, и запятую. Особо обратим внимание! В качестве разделителя между отдельными числами ни в коем
случае не следует использовать точку и запятую, так как эти знаки используются в качестве десятичного разделителя. Отделить
одно число от другого можно используя "пробел" или "ввод". Скажем, такой ввод в текстовое поле верен:
0,23 0,56 0.98
0,98 1,56 9,9 7.908
Соответственно будут обрабатываться семь значений: 0.23 0.56 0.98 1.56 9.9 7.908.